
| [ начало ] | [ В ] |
Волны
— Здесь описаны В.: а) водяные, б) воздушные звуковые, в) световые, г) электрические волны и д) математическая теория В.
А) Волны в воде обыкновенно являются следствием косвенного удара ветра о воду. Поверхность воды от этого делается вогнутой, но опустившиеся водяные частицы сейчас же возвращаются в первоначальные положения и, перейдя его, поднимаются, так что там, где было углубление, образуется выпуклость, потом опять вогнутость и т. д. Волнение передается соседним частицам и распространяется все дальше и дальше. Вопрос о роде движения водяных частиц во время волнения впервые решен экспериментальным путем братьями Э. и В. Веберами ("Die Wellenlehre auf Experimente gegr ü ndet", 1829). Полученные ими результаты впоследствии были подтверждены и дополнены исследованиями Гагена, Скотта, Росселя, Сен-Венана, Буссинеска, Эри и др. Братья Веберы производили опыты, пользуясь длинным и узким ящиком с боковыми стенками из зеркальных стекол. В ящик до ¾ высоты его наливалась вода, к которой примешивался порошок сургуча или плаунового семени — веществ, удельный вес которых мало отличается от удельного веса воды. На одном конце ящика в воду на небольшую глубину опускался конец особой трубки; ртом втягивали в нее воду и предоставляли последней падать обратно в сосуд. От этого толчка вода в ящике приходила в волнообразное движение. При этом отчасти с помощью циркуля, а отчасти с помощью грифельной доски, покрытой мукою, опускавшейся на мгновение в воду, причем на ней обнаруживался вид поверхности воды, определяли высоту волн, т. е. расстояние между наиболее высокой и наиболее низкой точками поверхности по вертикальному направлению, и длину волн, т. е. расстояние по горизонтальному направлению между выпуклостями или вогнутостями двух последовательных волн. С помощью часов определялась также скорость распространения волнообразного движения. Оказалось, что водяные частицы во время волнения движутся в вертикальной плоскости по эллипсам, большие оси которых горизонтальны, а малые вертикальны. В верхней части своего эллиптического пути частица движется по направлению распространения волн, а в нижней — по противоположному направлению. У поверхности воды эллипсы, описываемые частицами, близки к кругам, и размеры их наибольшие; чем глубже, тем они более вытянуты по горизонтальному направлению и тем они меньше. На некоторой глубине эллипсы превращаются в прямые линии, а несколько глубже частицы, находящиеся на различных глубинах, описывают пути различных величин: время оборота всех частиц одно и то же. Глубина распространения волнообразного движения зависит от высоты волн. Она, как оказалось из опытов Веберов, в 350 раз больше последней. Наконец, оказалось, что скорость распространения волнообразного движения увеличивается с увеличением длины и высоты волн (ср. далее В., математическая теория).
При взгляде на волнующуюся поверхность воды кажется, что частицы ее обладают быстрым поступательным движением. Передвигаются, и то незначительно, лишь возвышения и углубления, в состав которых, по мере их движения, постоянно входят все новые и новые частицы. Для уяснения этого представим себе, что волнение распространяется от левой руки к правой (черт. 1) и достигает частицы a, потом b, c, d и т. д.
Чертеж 1.
Первая начинает колебаться частица a, потом b, затем c и т. д. Каждая из них движется по эллипсу, близкому к кругу, притом так, что в верхней части своего пути идет слева направо, т. е. по направлению распространения волн, в нижней же обратно. В тот момент, когда частица a, совершив полный оборот, придет на прежнее место, частица b будет находиться не в своем первоначальном положении, а в некотором положении b1, частица c в положении c1 и т. д. Соединив точки a, b1, c1, d1...h1, k1, получим линию, которая даст понятие о виде поверхности воды в этот момент. Через некоторый промежуток времени после этого, например равный четверти времени оборота, частица a будет в a2, частица b — в b2, следующая из положения c1 перейдет в c и т. д. Вид поверхности воды в этот момент изобразится линией a2, b2, c1, d2... Впадина a, b1, c1, d1... передвинется в c, d2, f2, g2, h2... Возвышение e1, f1 g1... передвинется в h2, k2, l2... и вообще поступательно движутся лишь возвышение и углубление, которые на всем пути составляются все из новых и новых частиц воды. Из чертежа видно, что на возвышении водяные частицы движутся в сторону распространения волн, а в углублении — в обратную сторону. Обозначая через l длину волны, t — время оборота частицы, равное времени, в течение которого волнение распространяется на расстояние l, наконец через v — скорость распространения волн, т. е. расстояние, на которое передвигаются волны в одну секунду, получаем следующее равенство: l=vt.
В. в реках, озерах, морях и океанах обыкновенно происходят под влиянием ветра. Давление ветра не бывает однообразным на обширном пространстве: на некоторые точки поверхности он напирает сильнее, отчего здесь образуются системы В., вскоре слагающиеся в одну общую систему, направляющуюся по ветру. Сначала ветер производит небольшие В.; при дальнейшем действии его они постепенно увеличиваются. Так как ветер действует сильнее на заднюю сторону В., чем на переднюю, то, кроме колебательного движения, должно происходить в этом случае еще небольшое поступательное, что в действительности и наблюдается. Каждая частица совершает при этом путь, подобный указанному на чертеже 2.
Чертеж 2.
Для свободного движения частиц необходима большая поверхность и большая глубина. Этим объясняется, почему наименьшие В. наблюдаются в реках, а наибольшие — в океанах. Для определения длины В. устанавливают корабль по направлению движения В. Если длина В. меньше длины корабля, то замечают на корпусе корабля положения высших точек В. и расстояние между этими точками измеряют. Это и будет длина В. Если же длина В. больше длины корабля, то по часам замечают моменты, в которые две следующие одна за другой вершины В. достигают какой-нибудь точки корпуса корабля. Получаемый таким образом промежуток времени есть не что иное, как время оборота водяных частиц. Затем два наблюдателя определяют время, в течение которого какая-либо вершина В. доходит от одного конца корабля до другого. Разделив длину корабля на это время, найдем скорость В., а умножив последнюю на время оборота, получим длину В. (см. вышеприведенную формулу). При этом предполагалось, что корабль находится в покое. В противном случае надо принять во внимание скорость движения его, которая определяется лагом (см. это слово).
Для определения высоты В. наблюдатель влезает на ванты до тех пор, пока при самом низком положении корабля не увидит горизонта, т. е. пока его глаз не будет находиться на прямой, проходящей через вершины В. Высота глаза над поверхностью воды и будет, очевидно, высота В. О высоте В. у берега можно судить по футштоку. При суждении о высоте В. с корабля на глаз легко поддаться следующему оптическому обману: корабль во время волнения большую часть времени бывает в наклонном положении; наблюдатель, забывая об этом и видя надвигающийся на него вал, принимает за высоту его длину перпендикуляра, опущенного из вершины В. на продолжение палубы, что, очевидно, больше истинной высоты В. Это обстоятельство прежде упускалось из вида. Новейшие исследования дают высоты В. значительно меньшие, чем прежние. В открытых океанах длина В. редко бывает больше 140 метров. Впрочем, Мотец наблюдал в Атлантическом океане к северу от экватора — 824 метра. Весьма значительной длины В. удалось видеть также Джемсу Кларку (580 метров), близ мыса Доброй Надежды. Понятие о высоте океанских В. дает следующая таблица, составленная по Крюммелю и Парису:
|
Средняя, в м |
Наибольшая, в м |
Наименьшая, в м |
Отношение l:h |
|
| Атлантический океан, область пассатов |
1,9 |
6 |
0 |
35,2 |
| Индийский океан, область муссонов |
2,8 |
5 |
1 |
35,3 |
| Южный Атлантический океан, область W ветров |
4,3 |
7 |
1 |
31,0 |
| Индийский океан, область W ветров |
5,3 |
11,5 |
2,8 |
21,5 |
| Восточно-Китайское море |
3,2 |
6,5 |
0 |
24,6 |
| Восточная часть Тихого океана |
3,1 |
7,5 |
0 |
33,0 |
Здесь под h подразумевается высота В., l — длина их. Наиболее высокие В. в открытом океане наблюдали: Мисисси — у Азорских островов — 15 метров, Эберкромби — между Новой Зеландией и Южной Америкой — 14 метров. Если две или несколько систем В. сходятся, то происходит интерференция В. (см. Интерференция), причем местами волнение уменьшается, а местами усиливается. Влияние интерференции особенно значительно в центральной части урагана, куда сходятся системы В., идущие с разных сторон под влиянием различных направлений ветров, дующих в урагане (так называемая толчея). Волнение распространяется быстрее самых сильных ветров. Вот почему наступление его может служить признаком приближения бури.
Очень часто волнение выходит из области господства ветров, давших ему начало. Тут оно появляется в виде высоких и длинных медленно движущихся валов. Это явление называют зыбью. Особенно поразительно это явление при спокойном состоянии моря и слабом ветре, когда волн не видно, а между тем корабль испытывает качку. Зыбь происходит и тогда, когда ветер, произведший волны, стихает.
Если волна, идущая с глубокого места, встречает возвышенное дно, то движение ее замедляется, причем главным образом замедляется в нижней части, тогда как верхняя продолжает двигаться с прежней скоростью. От этого происходит внезапное увеличение высоты волны и вслед за тем опрокидывание ее. Это явление называется прибоем или буруном. В некоторых местах вид дна благоприятствует образованию прибоя, особенно в местах с подводными рифами и камнями, например на Мадрасском берегу, где волны прибоя достигают иногда 22 метров в высоту. Сильный прибой бывает также у западного берега экваториальной Африки, где он носит местное название "Калемы". Подобное же действие производят и крутые берега: волны, встречая их, поднимаются, следующие еще более возвышают их, так что они наконец падают назад. Во время бури такие волны взлетают на высоту нескольких десятков метров. Особенно больших размеров это явление достигает на берегах Суматры, на Фого — одном из островов Зеленого Мыса, на Нордкапе и проч. По причине прибоя кораблям нередко весьма опасно приставать к берегу.
В последнее время большое внимание обращено на действие масла на волны: масло, разлитое тонким слоем по поверхности волнующегося моря, понижает волны. Это происходит оттого, что в таком случае трение ветра о поверхность воды, а следовательно, и сила удара ветра меньше, так как ветер скользит по поверхности масла. Не все, однако, масла действуют одинаково. Лучше всего рыбий жир, например тресковый, а также жир китов, тюленей и дельфинов. Хорошо действует и неочищенная нефть, но в очищенном виде она почти бессильна против волн. Необходимо при этом выпускать масло понемногу, потому что только в таком случае оно разливается по поверхности воды ровным слоем. Обыкновенно масло вливают в парусинный мешок, в котором прокалывают небольшие отверстия и выставляют за борт на конце длинного шеста. Если нет под рукой парусинного мешка, можно налить масло в какой-нибудь вязаный мешок, набитый паклей. Наши матросы выставляют иногда за борт просто швабру, смоченную маслом.
Об этом свойстве масла упоминали еще древние ученые, например Аристотель, но только лет десять тому назад стали производить серьезные опыты для проверки этого свойства масла, и опыты увенчались полным успехом. Теперь во многих иностранных государствах предписано всем судам, отправляющимся в плавание, иметь масло и все нужное для выпускания его в море в случае бури.
Другая причина волн в океанах — землетрясения, происходящие близ берегов. Образующиеся от этого волны расходятся на громадные расстояния. Высота их мала, но длина очень велика; скорость распространения их весьма большая. Так, вследствие землетрясения, разрушившего город Симоду в Японии 23 декабря 1854 г., от Японии по Тихому океану пошли волны высотой около ½ метра и длиной в 390 метров, наблюдавшиеся 12½ часов спустя в Сан-Франциско и Сан-Диего. Скорость движения их равнялась 660 км в час. 26 августа 1883 года было извержение вулкана Кракатоа на Зондских островах, сопровождавшееся сильным землетрясением. Образовавшиеся от этого волны, высотой в 30—40 см, несколько раз обошли вокруг всего земного шара.
Эри дал интересный способ определения средней глубины океанов по скорости распространения таких волн. Для этого надо определить скорость распространения их по данному направлению и квадрат ее разделить на среднее ускорение силы тяжести по этому направлению. Таким образом, например, Гохштеттер на основании скорости распространения волн, происшедших от землетрясения в Симоде, нашел среднюю глубину Тихого океана между Японией и Сан-Франциско равной 4000 м, что хорошо согласуется с результатами непосредственных измерений глубин.
При том волнообразном движении, о котором все время говорилось, все водяные частицы, находящиеся в одной горизонтальной плоскости, описывают одинаковые пути, причем возвышение и углубление передвигаются. Но существуют волны, в которых различные частицы проходят различные пути, а возвышения и углубления происходят постоянно в одних и тех же местах, отделенных одно от другого частицами, не участвующими в движении. Такие В. называются стоячими, а неподвижные точки — узловыми точками (см. далее В., математическая теория). Стоячие В. образуются вследствие интерференции прямоидущих волн с отраженными. Их можно получить искусственно в приборе братьев Веберов. Вышеуказанным способом производят волны, которые, дойдя до концов сосуда, отражаются, идут назад и интерферируют с непосредственными волнами, отчего появляются стоячие волны, в которых частицы кажутся подымающимися и опускающимися против одних и тех же мест. Подобное колебательное движение происходит иногда в некоторых озерах и морях, например в Женевском озере, Охриде в Албании, в озере Веттер, в Адриатическом море и проч. Это явление называется сейши (Seiches). Сейши Женевского озера обстоятельно изучены Форелем, Адриатического моря — Гратцлем. Сейши Женевского озера состоят в том, что уровень озера в течение 30—40 мин. поднимается, затем столько же времени опускается, потом опять поднимается и т. д.; это продолжается некоторое время. Форель нашел, что это есть не что иное, как стоячие волны с одной узловой точкой, отчего колебания на двух противоположных берегах — в Женеве и Вильневе противоположны, т. е. в то время, как в Женеве уровень воды поднимается, в Вильневе опускается и наоборот. Основная причина сейшей — ветер, производящий обыкновенные волны, которые после отражения от берегов дают отраженные; эти последние с первыми и производят стоячие волны. В океанах и морях наблюдаются еще так называемые приливные волны — следствие притягательного действия Луны и Солнца на Землю (см. Приливы и Отливы).
Литература указана подробно в книге: Bogusł awski-Krümmel, "Hand buch der Oceanographie", 2 тома, 1884—1887.
П. Броунов.
Б) Волны звуковые. Звуковые впечатления образуются вследствие приведения барабанной перепонки уха в дрожательное состояние прилежащими к ней слоями воздуха (см. Звук), который сам приведен в колебательное движение соответственным способом, например колебаниями камертона, струны, колокола. Упругая пластинка, получившая удар молоточком, гонит воздушные частицы то в ту, то в другую сторону и тем заставляет их сближаться между собой, т. е. образует по обе стороны в воздухе уплотненные слои. В то же время со стороны, противоположной направлению движения камертона, образуется разрежение воздуха. Образующиеся сгущения и разрежения передвигаются вперед по сообщенному им направлению и в стороны, но воздушные частицы движутся только взад и вперед, между сравнительно недалекими пределами, которые тем ближе, чем больше высота тона, соответствующая движению. В то время, когда одни воздушные частицы идут вперед, другие возвращаются назад, — что происходит попеременно, как изображено на чертеже 3 (I, II, III), на котором также можно видеть последовательное перемещение волны слева направо.
Чертеж 3.
Частицы, идущие навстречу друг другу, сближаются и производят сгущенные слои (a, c, e); частицы, удаляющиеся одна от другой, образуют разреженные слои (b, d). Эти сгущенные и разреженные слои передаются вперед, составляясь все из новых и новых частиц (черт. 3, II и III). В действительности же, вследствие перемены прямого движения частиц в обратное, сгущения обращаются в разрежения, а разрежения — в сгущения (черт. 3, I и III). Ряд частиц, составляющих один сгущенный и один разреженный слой и между ними слой нормальной плотности, составляет воздушную звуковую волну. Переход от сгущенного слоя к разреженному постепенен. Длина этого ряда, т. е. расстояние от одного сгущения до другого есть длина волны. Чем больше число колебаний (в секунду) звучащего тела, тем короче волны; воздушные частицы каждой волны не выходят из ее пределов при своих колебаниях. Расстояние, на котором образуются волны в воздухе в продолжение одной секунды, составляет около 340 метров (при 16° Ц.), через две, три секунды колебательное движение передается на двойное или тройное расстояние. Эта скорость передачи не зависит от числа волн или от числа колебаний звучащего тела, поэтому длина звуковой волны может быть найдена разделением 340 метров на число колебаний звучащего тела; это последнее число определяется различными способами (см. Звук). Вообще, называя длину звуковой волны буквою l, число колебаний или волн в секунду — буквой n, a скорость распространения волн через v, получим, как следствие сказанного выше, v=nl. Допуская, что музыкальные тоны фортепиано заключаются между 271½ и 3500 колебаниями, заключаем отсюда, что длина соответственных звуковых волн содержится между 12,363 м и 97 мм. Длина волны самой низкой басовой ноты человеческого голоса, когда-либо слышанной на театральной сцене, составляет 5,573 м, а самого высокого сопрано 260 мм и даже (одной певицы прошедшего столетия) 170 мм. Длина волны нормального камертона в 435 колебаний составляет при 16° Ц. 781,6 мм. На протяжении каждой звуковой воздушной волны частицы воздуха, сдвинутые со своего места, находятся последовательно в различных удалениях от нормального их положения, которое они занимали до начала движения. Эти различные их удаления изображаются чертежом (черт. 4, II).
Чертеж 4.
Выпуклая часть кривой линии показывает удаление частичек, сдвинутых в сторону распространения движения, вогнутая — сдвинутых в противоположную сторону; частицы в начале, середине и конце линии вовсе не сдвинуты с места. Вся линия, имеющая волнообразный вид, наглядно изображает величину сдвига ряда воздушных частиц, составляющих волну. Такое изображение звуковой волны, хотя и символическое, представляет большие удобства для наглядного ознакомления со свойствами волн, в особенности в случаях содействия двух или более волн (см. Интерференция), когда волны или усиливают друг друга, или, напротив, взаимно ослабляются и даже уничтожаются. Символическая форма волны, составленной из двух, трех или большего числа волн, может весьма отличаться от формы составляющих.
Высота выпуклости и глубина вогнутости символической звуковой волны, представляющая наибольшие удаления частицы от ее положения равновесия, вместе с тем указывает на большую или меньшую силу звука, зависящую от величины размаха частиц во время их колебаний. При составлении сложной волны высоты составляющих волн имеют существенное влияние. Например, звук всякой струны есть сложный, состоящий из главного, господствующего тона и значительного числа высших гармонических тонов, которые, изменяя характер главного, придают ему особенный оттенок (Klangfarbe). Форма звуковой В., происшедшей от колебания струны, будет весьма сложная (см. Звук, Струны, их колебания), колебания фортепьянной струны отличаются от скрипичных и т. д. Очень сложны также волны, происходящие от звуков человеческого голоса. Доказано, что при произношении — и лучше всего нараспев — гласных букв тон, издаваемый горлом человека, будучи основным, непременно сопровождается высшими тонами.
Наибольшую простоту имеет звуковая волна камертона, изображающаяся символически синусоидой (фиг. 4, II); наибольшую же и — можно сказать — беспорядочную сложность представляют различные шумы и вообще немузыкальные звуки. Однако всякая сложная волна может быть рассматриваема как сумма простых волн (синусоид). Ухо человека во многих случаях может в сложной волне ощущать составные ее части; музыкант, слыша аккорд, легко называет составные ноты. Это значит, что сгущения и разрежения сложной волны, производя давление на барабанную перепонку, сохраняют характер суммы давлений от каждого отдельного составляющего звука; орган слуха замечателен способностью воспринимать отдельные впечатления в более или менее сложной сумме (см. Слух).
Особый вид волн суть стоячие волны (см. далее, а также Интерференция). Органные трубы (см.) во время звучания содержат в себе стоячие волны; происходящие в них сгущения и разрежения могут быть ясно показаны на опыте, так как они происходят постоянно в одном и том же определенном месте трубы.
Сложность геометрической формы линии, символически выражающей сложную звуковую В., в действительности выражается особенностями в сгущениях и разрежениях. Изучению этих особенностей мог бы способствовать фонограф (см. это слово), который механически отмечает колебательные движения пластинок, происходящие от звуковых воздушных волн. Знаки, оставляемые штифтом прибора на воске или листовом олове, так мелки, что для исследования их нужно употребление микроскопа.
В) Волны света и тепла. Волны в жидкостях могут быть видимы и осязаемы; воздушные разрежения и сгущения в звуковых волнах могут быть показаны опытом; существование световых и тепловых волн есть гипотеза, хотя в высшей степени правдоподобная, но доказываемая лишь косвенными способами. Наука принуждена допустить существование эфира, вещества чрезвычайно тонкого и упругого, которого частицы, будучи приведены в колебательное движение, производят все световые и тепловые явления (см. Свет, Эфир). Различие между колебаниями эфирных и воздушных частиц полагается в том, что вторые двигаются по направлению распространения волн, эфирные же частицы колеблются перпендикулярно направлению луча света. Рассуждая о колебаниях эфирных частиц, первоначально расположенных на прямой линии, надо себе представить, что все они одна за другой последовательно удаляются от этой линии на некоторое расстояние, затем приближаются к ней для того, чтобы потом удалиться по другую ее сторону. Если б можно было видеть эти эфирные частицы в некоторый момент, то оказалось бы, что они расположены по синусоиде (см. чертеж 4), которая в этом случае не есть символическое представление волны, как то было для звука, но действительное очертание В. Скорость распространения колебаний эфира или скорость света (см. это слово) составляет около 300000 км в секунду в пустом пространстве. Подобные волны могут образоваться и внутри тел (прозрачных), в промежутках между их частицами, но распространяются с меньшей скоростью, чем в пустоте.
Колебательные движения, возбужденные в какой-нибудь точке пространства, наполненного эфиром, распространяются во все стороны с одинаковой скоростью в среде однородной, как, например, в воздухе, воде, стекле, так что образуют волну шаровой поверхности. Если же тело неоднородно, т. е. имеет по различным направлениям различную плотность, упругость и другие свойства, то и поверхность волны будет не шаровая. В очень многих кристаллах световая волна, падающая на них, положим, из воздуха, разделяется на две волны внутри кристалла, идущие вообще по разным направлениям и с различной скоростью. В так называемых одноосных кристаллах (пример: исландский шпат) одна волна имеет шаровую форму другая — эллипсоидальную (см. Двойное лучепреломление). Световые волны могут быть неодинаковой длины, которая во всяком случае чрезвычайно мала. Волны неодинаковой длины производят различное действие на зрительные нервы; волны, производящие ощущение красного цвета, длиннее волн, соответствующих фиолетовому цвету. Впечатления простого (спектрального) желтого, зеленого и синего цвета происходят от волн, которых длина есть промежуточная между длинами двух вышеназванных волн. Если несколько световых волн действуют совместно на зрительные нервы, то производят впечатление сложного цвета, которому соответствует в музыке аккорд. Белый цвет составляется содействием всех волн, соответствующих простым цветам спектра; соответственное звуковое впечатление от действия многих тонов, лежащих рядом, есть шум. Гипотеза существования световых волн лучше всего подтверждается многочисленными и разнообразными явлениями интерференции света (см. это слово). Сущность интерференции света та же, что для интерференции всяких других волн; две световые волны могут не только усиливать одна другую, но и взаимно ослабляться и даже уничтожаться. Другими словами: свет, прибавленный к свету, может произвести темноту, — парадоксальное на первый взгляд заключение, но неопровержимо доказанное опытами.
От величины размаха эфирных частиц зависит подъем (высота) волны и сила производимого ею светового впечатления. Мы не имеем никакого понятия о высоте световых волн, но длина их хорошо измерена на основании многих явлений интерференции. Самая длинная световая волна (соответствующая темному красному цвету) занимает всего 0,00076 мм длины; такой величины предмет, будучи наблюдаем в микроскоп, увеличивающий около 1300 раз, принял бы кажущуюся длину всего в 1 миллиметр. Явления теплового лучеиспускания объясняются также образованием эфирных волн, так как распространение, отражение, преломление тепловых лучей и много других явлений тепловых лучей происходят совершенно одинаково с соответственными световыми явлениями. Но тепловые волны, исходящие от теплых (т. е. нагретых, но не накаленных) предметов, длиннее световых волн; самая длинная до сих пор измеренная тепловая В. с лишком в семь раз длиннее самой длинной световой длины; но есть основание предполагать, на основании показаний болометра (см.), что существуют волны еще впятеро длиннейшие; тепловым волнам также свойственны явления интерференции и различные особенности при образовании внутри кристаллов, вполне соответствующие особенностям световых волн. Волны светового эфира способны возбуждать различные химические изменения вещества, в особенности короткие, синие (говоря так для краткости) и фиолетовые, волны. За пределами самых коротких волн, производящих световое впечатление, находятся еще более короткие волны, сильно возбуждающие химические действия. Это свойство их дает возможность фотографировать невидимую часть спектра. Если назвать эфирные волны, соответствующие этой части спектра, химическими и сравнить длину самой короткой химической волны с самой большой длиной тепловой волны, то найдем, что вторая превосходит первую в 150 раз.
Ф. Петрушевский.
Г) Волной электрической или электромагнитной называется система возмущений середины, окружающей проводник электричества, возникающая в ней, когда в проводнике происходит правильно чередующаяся перемена зарядов положительного электричества на заряды отрицательные. Подобные же пертурбации происходят и в случае разрядов между внутренней и внешней обкладками лейденской банки, чередующихся по направлению (колебательный разряд — см. это слово). Эти пертурбации распространяются в непроводнике (в воздухе) со скоростью передачи световых и тепловых волн, следовательно, обуславливаются эфиром. Расстояние, на которое передается вперед движение в промежутки между двумя одноименными (положительными или отрицательными) зарядами проводника или между двумя в одну сторону идущими разрядами лейденской банки, составляет длину электрической волны. Эта длина зависит от размеров и формы проводников. Электрические волны давно предусмотрены теорией, но опытным путем, при длине волн от 60 см до 10 м, они обнаружены лишь несколько лет назад профессором Герцем (в Бонне), при помощи колебательных разрядов в катушке Румкорфа (см. это слово). Электрические волны (удобно получаемые в 5 м длины) обнаруживаются световыми явлениями в так называемых электрических резонаторах (особые проволочные кольца, в одном месте перерезанные); они, подобно световым, могут отражаться, преломляться и интерферировать между собой. Ср. Теория света, Максвелл, Герц. Мы встречаемся с длинами одного порядка со звуковыми волнами.
Д) Волны (математическая теория) уединенные, последовательные и стоячие. Волной называется временная деформация (см. это слово) части сплошного тела, произведенная в одном месте его и распространяющаяся последовательно через остальные. Примерами могут служить: распространение волн вдоль по гибким нерастяжимым шнурам, движения волн по поверхности жидкости, распространение звуковых волн в воздухе. В первом случае волны распространяются по одному протяжению — длине нити, во втором могут распространяться по двум протяжениям поверхности жидкости, в третьем — по трем протяжениям объема воздуха.
Несмотря на то, что учение о волнообразных движениях играет очень важную роль в современной натуральной философии, оно еще мало разработано и математические теории его по большей части приближенные. В. разделяют на три класса: уединенные, последовательные и стоячие.
Уединенные волны. Говоря о распространении уединенных волн, приходится упоминать: о виде и пределах деформации, представляющей уединенную волну, о скорости движения В. или частей ее и о движении каждой точки тела при прохождении В. через эту точку. Если длинную гибкую веревку держать за оба конца так, чтобы она была слабо натянута и по возможности мало выгнута, то надлежащим быстрым и коротким движением одного из концов ее можно возбудить в ней уединенную В. произвольного вида, которая пройдет до другого конца с постоянной скоростью. Теоретически этот случай рассматривается следующим образом. Представляют себе гибкую однородную нерастяжимую веревку невесомой и прямолинейной в состоянии покоя, причем натяжение ее N постоянно по всей длине; так как веревка однородна, то и линейная плотность ее μ (т. е. отношение массы какой-либо части длины веревки к величине этой длины) постоянна по всей длине веревки. Деформации веревки предполагаются столь малыми, что возникающие при них изменения натяжения Δ N ничтожны сравнительно с N, так что уже квадратами отношений Δ N/N можно пренебречь. При таком приближении окажется:
1) что уединенная В. движется по веревке с постоянной скоростью, равной
V = √(N/ μ) (1)
2) что, при прохождении В., точки оси веревки должны совершать ничтожно малые движения поперечные (т. е. перпендикулярные к первоначальному положению прямолинейной оси веревки;
3) что вид самой В. может быть произволен, но кривая, образуемая ею, не должна иметь изломов
4) что вид В. сохраняется без изменения.
Результаты получатся иные, если предположить веревку тяжелой и первоначально повешенной вертикально за один конец ее. Тогда скорость прохождения В. через каждую точку оси веревки выразится той же формулой (1); но теперь натяжение веревки в какой-либо точке оси ее равняется весу частей, находящихся ниже этого места, а потому скорость возрастает при распространении В. вверх и убывает при распространении вниз; из этого следует, что длина, занятая уединенной В., увеличивается при движении В. вверх и уменьшается при движении ее вниз. Обратимся теперь к распространению уединенной В. жидкости в канале с прямоугольным сечением. Такая В. образуется если на одном конце канала будет погружено достаточно быстро тело значительных размеров. На существование таких В. обратил внимание Скотт Россель (Russel) в 1844-м году, а приближенные теории их были даны Буссинеском ("Theorie des eaux courantes") и лордом Рейлейем (Rayleigh, "Philos. Mag.", 1876). Пренебрегая высшими степенями отношения высоты В. к ее длине, Рейлей находит: 1) что скорость ее движения равна
√q(h + β),
где g есть ускорение силы тяжести, h — глубина канала и β высота В. над первоначальным горизонтом; 2) что вид уединенной В. таков, как на чертеже 4, (I), где XX есть горизонт воды в канале, ABC — вид сечения поверхности В. вертикальной плоскостью, DB — высота В.; стрелки под линиею XX означают направление движения В. Эта уединенная В. не имеет границ, так что кривая ABC только асимптотически приближается к горизонту XX. Точки жидкости при движении уединенной В. описывают параболические дуги, симметричные относительно вертикальных осей; например, точка жидкости, находящаяся при положении В., представленном на черт. 4 (I), в точке B, на вершине волны, описала уже параболическую дугу MB, а при дальнейшем движении опишет дугу BN; длина перемещений MN по горизонтальному направлению всех точек жидкости, как на поверхности, так и ниже ее, одинакова и равна отношению объема В. к глубине канала; высоты же параболических дуг пропорциональны расстояниям точек от дна канала.
Последовательные В. образуются в гибкой, нерастяжимой, длинной, слабо натянутой и почти горизонтальной веревке, если одному из концов ее будет сообщено поперечное периодическое движение произвольного характера и произвольного периода. Тогда по веревке пойдет ряд последовательных В. того же периода, со скоростью, свойственною уединенной В. При рассмотрении последовательных В. придется говорить не только о виде В., скорости распространения их и о движении каждой точки тела, но, кроме того, еще о периоде полного колебания каждой точки и длине В. В рассматриваемом случае движения всех точек оси веревки суть периодические поперечные колебания; если T есть продолжительность одного полного колебания, λ — длина В., то эти две величины связаны со скоростью V распространения волн следующим равенством: VT= λ.
Последовательные волны самого простейшего вида получаются при простом гармоническом колебании (см. Гармонические колебания) конца веревки, выражаемом следующим уравнением:
η o = A sin2 π t/T (2)
где ηo есть величина отклонения конца в момент t, A есть амплитуда гармонического колебания, т. е. наибольшее отклонение колеблющейся точки в одну сторону. Движения точки, отстоящей на длину x от конца по оси веревки, будут выражаться уравнением:
η = A sin2 π (t/T — x/ λ) (3)
где η — поперечное отклонение этой точки в момент t от ее положения равновесия. Для одного и того же момента t и для всевозможных x уравнение (3) выражает кривую линию, представляемую веревкой в этот момент. Кривая эта есть синусоида: она изображена на чертеже 4 (II). Эта кривая, не изменяя своего вида, подвигается равномерно по оси Х 1 Х 2 в сторону, указанную стрелкой. Уравнение (3) есть только частное решение дифференциального уравнения:
d2η/dt2 = V2dη/dx2 (4)
малых поперечных колебаний прямолинейно натянутой гибкой веревки; мы здесь не останавливаемся над общим решением его, так как это потребовало бы много места.
Полного решения вопроса о распространении волн по поверхности жидкости не имеется; но некоторые частные случаи разработаны теоретически более или менее подробно.
Pacnpocmpaнeниe последовательных волн по длине канала прямоугольного сечения и произвольной глубины и морских волн с прямолинейными гребнями. Этот вопрос рассматривался Лагранжем, Пуассоном, Коши, Грином, Эйри и Стоксом. Наиболее полное решение принадлежит последнему (Stokes, "On the theory of oscillatory wawes", "Mathematical and physical papers", т. I). Так как здесь будут приведены уравнения поверхности волн, то условимся, что начало координат взято посередине канала, в горизонте покоящейся жидкости, что положительная ось Х направлена горизонтально посередине канала в сторону распространения волн, ось Z — горизонтально поперек канала и положительная ось Y вниз. Глубина канала или моря равна h, σ — плотность жидкости, g — ускорение силы тяжести; u и v — скорости точек жидкости в направлениях параллельных осям X и Y; p — давление на единицу поверхности. Скорости в направлении оси Z полагаются равными нулю. Движение предполагается без вихрей или частичных вращений, так что скорости предполагаются имеющими потенциал φ, и следовательно:
u = d φ /dx, v = d φ /dy
u, v, φ и p суть функции от x-ct и y, где t есть время и c — скорость распространения волн. Предполагая движение малым, оказывается, что скорость распространения зависит следующим образом от длины волн λ и от глубины дна h:
c2 = g λ /2 π tghyp ∙ 2 π h/ λ (5)
где гиперболический тангенс от какой-либо величины q означает следующее отношение:
tg hyp ∙ q = (eq — e-q)/(eq + e-q);
в формуле (5) вместо q надо подставить отношение 2π h: λ.
Если канал очень мелок, а волны настолько длинны, что можно пренебречь вторыми и высшими степенями отношений h: λ, то формула (5) даст следующую скорость распространения длинных волн на мелких местах:
отсюда видно, что эта скорость не зависит от длины волн, но только от глубины дна. Если же, напротив, глубина дна так велика сравнительно с длиной волн, что можно положить λ:h равным нулю, то формула (5) даст следующую величину скорости распространения морских волн:
Следовательно, скорость морских волн пропорциональна корню квадратному из длины их. Чтобы не приводить слишком длинных выражений, ограничимся следующими выражениями, относящимися ко второму приближению для морских волн.
Уравнение контура волнообразной поверхности в какой-либо момент t:
y = a cos2 π / λ (x — ct) — a2 π / λ cos4 π / λ (x — ct) (8)
где 2 a есть высота гребня волны над нижней точкой ее углубления. Мы ниже представим вид волны при третьем приближении, а теперь заметим: 1) что высота ее гребней над горизонтом равна a(1+a π / λ), а глубина — a(1-a π / λ); 2) что в местах пересечения с горизонтом ширины валов менее ширины углублений.
Если x и y суть координаты какой-либо точки жидкости в состоянии покоя, а x+ ξ и y+ η координаты ее же в момент t, то во втором приближении:
ξ = ae-ny sin2 π / λ (x — ct) + s
η = ae-ny cos2 π / λ (x — ct)
где
n = 2 π / λ, s = a24 π 2/ λ 2 ∙ cte—2ny.
Если бы не было в выражении для ξ добавочного члена s, то из формул для ξ и η следовало бы, что каждая точка равномерно описывает около своего положения окружность радиуса ae-ny в течение периода, соответствующего времени прохождения длины волны. Точки, находившиеся на верхнем горизонте воды, описывают окружности радиуса a, а вглубь — радиусы окружностей уменьшаются в геометрической прогрессии. Присутствие члена s показывает, что к этим движениям присоединяется весьма медленное равномерное перемещение точек жидкости в сторону распространения волн, наибольшее для точек поверхности и быстро уменьшающееся для слоев более углубленных.
В третьем приближении уравнение контура морских волн следующее:
y = a cosn (x — ct) — ½a2n cos2n (x — ct) + ⅜a3n2 cos3n (x-ct) (9).
На чертеже 4 (III) изображен вид этой кривой для случая 80a=7λ; она весьма близко подходит к виду растянутой циклоиды.
Трохоидальные волны Герстнера. В 1802 г. Герстнер придумал теорию волн, которая потом была разработана Ренкиным.
Этот весьма замечательный случай волнообразного движения при бесконечно большой глубине дна представляет частное точное решение дифференциальных уравнений гидродинамики в виде, данном им Лагранжем. Координаты какой-либо точки жидкости в момент t выражаются в этом движении следующими функциями времени и координат a и b той же точки в момент t=0.
x = a + r sin θ и y = b + r cos θ (10)
где r = Re — nb,
θ = 2 π / λ
(a — ct), n = 2 π / λ,
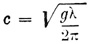 и R не более
1:n.
и R не более
1:n.
При этом давление в какой-либо точке выразится следующим образом:
p = po + g[b — π / λ R2(1 — e)-nb]
так что на свободной поверхности, где b =0, давление равно po; в каждой точке жидкости давление не изменяется при ее движении и поверхности равного давления суть те, на которых b имело одну и ту же величину. Кривая свободной поверхности сечения плоскостью XY выражается уравнениями:
x — ct = R sin θ + θ /n
y = R cos θ.
Это есть растянутая циклоида, описанная точкой, отстоящей на длину R от центра круга радиуса 1: n, катящегося без скольжения по прямой параллельной оси X и находящейся выше ее на длину 1: n.
При этом движении в каждом месте жидкости происходят вихревые вращения, вращательные скорости которых имеют наибольшую величину на свободной поверхности и быстро уменьшаются в глубине.
Последовательные волны в канале с треугольным сечением. Келланд в 1841 году решил вопрос о движении волн вдоль по каналу, берега которого спускаются под углом в 45°, так что поперечное сечение канала есть равносторонний треугольник, имеющий вершину на глубине h под основанием, совпадающим с уровнем спокойной воды. В этом случае скорость распространения волн вдоль канала также выражается формулой (5), но В. уже не цилиндрические, так что сечения их вертикальными плоскостями, перпендикулярными к длине канала, суть не горизонтальные прямые, а цепные линии, вершины которых находятся над серединой канала. Внутреннее трение жидкостей не изменяет заметным образом скорости распространения В., но уменьшает постепенно высоты их. Если две системы В. одинаковой высоты и мало разнящейся длины распространяются в одном направлении, то, взаимно интерферируя, образуют группы В., разделенных промежутками спокойной воды; в каждой группе идут В. прогрессивно возрастающие от краев группы к ее середине, где В. достигают двойной высоты. Скорость распространения групп составляет половину скорости распространения самих В., если глубина жидкости бесконечно велика; на мелком же месте скорость групп равна скорости В.
Стоячие волны не подходят под данное в начале этой статьи определение понятия о В., потому что при них все точки тела одновременно совершают колебания около положений равновесия; но такие колебания можно рассматривать, как результат интерференции (см.) последовательных В. с отраженными от границ тела.
Дифференциальное уравнение поперечных колебаний гибкой нерастяжимой нити данной длины l, концы которой неподвижны, есть то самое уравнение (4), которое приведено выше; но в настоящем случае необходимо, чтобы η было равно нулю во всякий момент времени на концах, т. е. при x = 0 и при x = l. Такому условию частное решение (3) не удовлетворяет, но может удовлетворить следующая сумма:
A sin2 π (t/T — x/ λ) + B sin2 π (t/T + x/ λ)
если подобрать коэффициенты B и A и величину λ так, чтобы условия неподвижности концов были удовлетворены. Для того, чтобы эта сумма была равна нулю в конце x =0 надо, чтобы было A+B =0, а поэтому, чтобы та же сумма была равна нулю и в конце x=l, необходимо, чтобы было:
sin2 π l/ λ = 0.
Последнее означает, что λ должно быть равно одной из следующих величин: 2 l, 2l/2, 2l /3, и вообще 2l:n, где n — целое число. Так как TV= λ, то продолжительность стоячего колебания нити может иметь одну из следующих величин:
Уравнение же колебания нити при выбранном целом числе n будет такое:
η = 2A sinn π x/l ∙ cos2 π t/T (12).
Из этого уравнения видно, что точки нити, соответствующие x равным l/n, 2l/n, 3l/n...(n—1)l/n, будут неподвижны; эти точки называются узлами стоячей волны. Во всякий момент движения нить имеет форму синусоиды, проходящей через узлы и амплитуда которой периодически изменяется между пределами: +2 A и —2 A; точки нити, отклоняющиеся на величины ±2 A от положения равновесия, называются пучностями и находятся на серединах интервалов между узлами.
Вопросами о стоячих колебаниях тяжелых жидкостей занимались С. Венан, Кирхгофф, Greenhill; последние решили некоторые вопросы о стоячих колебаниях в канале треугольного сечения, при которых узловые линии параллельны длине канала. С. Венан нашел два приближенных частных решения дифференциальных уравнений движения, выражающих два рода стоячих колебаний, наблюдаемых на море; в одном из них (clapotis, зыбь) все точки жидкости колеблются прямолинейно, точки, находящиеся в пучностях — по вертикальным, а в узлах — по горизонтальным прямым; в другом (houle, толчея) — точки описывают эллипсы, а при большой глубине — круги, размеры которых уменьшаются в геометрической прогрессии для слоев, находящихся в глубине.
Д. Бобылев.
|
Page was updated:Tuesday, 11-Sep-2012 18:14:57 MSK |