— греческий геометр; родился приблизительно за 370 л. до Р. Х. и принадлежал к числу учеников Платона; он занимался исследованиями конических сечений, но труды его не дошли до нас. Своей известностью он обязан указанию на возможность спрямления круга с помощью кривой, известной геометрам до него и служившей для деления окружности на части, пропорциональные отрезкам прямой.

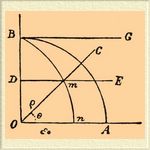
Кривая эта получила впоследствии название квадратриссы Д. и может быть построена следующим образом: пусть радиус OC вращается равномерно около точки О по направлению от А к В, при чем дуга AB составляет четверть окружности; пусть прямая DE движется также равномерно, оставаясь параллельной ОА; при этом пусть скорости движения ОС и DE таковы, что, оставляя одновременно положение ОА, они приходят одновременно в положение OB и BG. Геометрическое место точек пересечения радиуса ОС и прямой DE и есть квадратрисса. Из происхождения кривой с очевидностью вытекает известное еще грекам свойство ее; кроме того, легко видеть, что уравнение кривой в полярных координатах будет:

π/(2θ) = OA/(ρsinθ) или (π/2)ρ = ОА (θ /sin θ),

а отсюда ясно, что π/2 = OA/ρ ₀,

где ρ ₀ = On есть значение радиуса вектора ρ при θ = 0; таким образом, действительно, квадратрисса Д. дает способ спрямления окружности.