(diffraction, inflexion, Beugung, уклонение света). — А) явление световой Д. Объяснение ее Ньютоном. Принцип Гюйгенса. Объяснение Д. Френелем. В) плоская дифракционная сетка. Вогнутая сетка Роуланда. С) таблица длины волн. D) явление Д. в зрительных трубах. Е) звуковая Д.

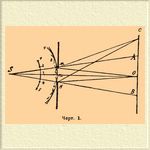
А) Дифракцией называется свойство световых лучей образовывать чередующиеся полосы и кольца после того, как лучи от светящейся точки или линии обойдут края непрозрачных небольших предметов (игла, волос) или пройдут через небольшие отверстия (узкая щель, сетка). Гримальди (XVII в.) первый наблюдал такие полосы по краям тени от ширмы, на которую падали солнечные лучи через узкое отверстие. Гримальди объяснил себе происхождение полос особым уклонением лучей, назвав это явление дифракцией. Одно из типичных и легко наблюдаемых явлений Д., представляющее ряд радужных изображений свечи или лампы, получается, если смотреть на пламя через прищуренные ресницы с расстояния 4-5 м. Мы легко также замечаем особенным образом распределенные полосы и сияние около пламени уличного фонаря или свечи, когда смотрим на огонек через ткань носового платка... Долгое время после Гримальди при описании дифракционных явлений ограничивались только предположением, что лучи изгибаются, когда минуют края экранов или проходят через малые отверстия. Ньютон приписывал этот уклон лучей притягивающим и отталкивающим силам, которые, по его мнению, должны бы существовать между частицами светящейся материи в луче и краями экранов. Гипотеза эфирных волн во времена Ньютона тоже не в состоянии была объяснить ни световой тени, ни чередования света с темнотой в дифракционных полосах. Все последующие опыты, однако, доказывали, что изгиб световых лучей увеличивается всегда с уменьшением экранов и отверстий и что характер дифракционных полос и относительное их распределение зависят от формы краев экрана и цвета лучей, но нисколько не зависят от вещества экрана. Френель в двадцатых годах нынешнего столетия, воспользовавшись идеями Гюйгенса и Юнга относительно сущности светового луча, первый дал верное объяснение Д. в знаменитом своем мемуаре, премированном Парижской акад. наук в 1 8 19 г. (Fresnel, "Oeuvres complètes" t. I, p. 247). Объяснение Френеля основано на применении принципа интерференции к элементам одной и той же поверхности волны. По принципу Гюйгенса, каждая точка (1, 2, 3...) сферической поверхности световой волны (черт. 1) является самостоятельным центром новых сферических волн 1, 2, 3..., огибающая которых представляет новое положение поверхности волны MmN (см. Свет — теория).

Черт. 1.

Френель дополнил принцип Гюйгенса следующим замечанием. Каждая точка А, внешняя относительно поверхности волн, испытывает слагающееся колебание от всех точек этой поверхности, но каждое из слагающих колебаний в такой внешней точке А (черт. 2) имеет особую фазу в зависимости от расстояния А до различных точек M, n, m, p и N поверхности волны KL.

Черт. 2.

Если расстояния отличаются друг от друга на одну или на несколько волн (четное число полуволн), то соответственные слагающие колебания будут совпадать в своих фазах (см. Интерференция). При разности в расстояниях на 1/2 волны или на нечетное число полуволн соответственные слагающие колебания будут приходить в внешнюю точку в противоположных фазах. Если принять во внимание это френелевское дополнение к принципу Гюйгенса, то делается очевидным, что для каждого элемента поверхности волны около каждой из точек вроде m, n или о всегда существует на ближайшем расстоянии от него другой соседний элемент, противодействующий первому. Принимая длину эфирных световых волн чрезвычайно малой (около 1/2000 мм), всегда можно для данной точки А выбрать такой ряд последовательных точек (m, n, М) на поверхности волны, расстояния которых до А будут отличаться друг от друга попарно на 1/2λ (т. е. пА - тА = λ/2, nA - МА = λ/2 и т. д.). Таким образом, лучи от всех элементов поверхности волны KL будут противодействовать друг другу за исключением лучей одного элемента m, пересекаемого прямой SA. Руководствуясь этими соображениями, Френель объяснил все основные явления Д. света, а именно:

1) Дифракция от узкой щели MN (черт. 1), когда получаются от светящейся линии S полосы в плоскости AB. Если разность хода лучей NA и MA равна четному числу полуволн [2n(λ/2)], то действующую через отверстие MN часть поверхности волны можно разделить на четное число элементов, которые будут попарно противодействовать друг другу, а следовательно, обусловят minimum света в точке А. При

NA — MA = (2n + 1)(λ/2)

в А будет светлая полоса, так как действующая часть поверхности волны будет заключать нечетное число элементов, а следовательно, один из них не будет иметь себе парного элемента и обусловит maximum света для точки А. В точке О (прямо против отверстия) может быть или сконцентрированный свет, или же образуется темное место, смотря по тому, насколько разнятся по ходу лучи No и mo, Mo и mo. Если

то в О темнота; а при разности хода

в точке О усиленный свет. Пользуясь принципом Гюйгенса, Френель мог рассчитать заранее или размер круглого отверстия MN или расстояния Sm и тА (черт. 2), при которых от светящейся точки S получается в светлом круге в точке А или темнота, или усиленный свет. На черт. 2 показано, что действующая часть волны заключает в себе 4 элемента, противодействующие друг другу попарно (Мп противодействует пт, Np — противодействует рт). Если уменьшить отверстие до M'N', то в А получится усиленный свет, так как исключится противодействующее влияние элементов Мп и Np.

2) Дифракционные полосы от маленькой прямоугольной ширмы MN, которые образуются внутри и вне тени (черт. 3).

Черт. 3.

Внутренние полосы, п o Френелю, происходят от интерференции элементов поверхности волны по сторонам ширмы, а внешние р ₁, p₂ обусловливаются интерференцией лучей от частей поверхности волны, лежащих по одну сторону ширмы, а именно: полосы около р ₁ — от интерференции лучей от М'М" и М'М, a полосы около p₂ — от NN' и N'N". Если закрыть действующую часть волны с одной стороны вполне, продолжив ширму MN до N", то останется только одна система полос около р ₁ — на краю тени.

3) Опыт Юнга (Young). Если в сплошном экране сделать две прямоугольные щели, которые приходились бы как раз на месте элементов М и N (черт. 3), то через такие 2 щели свет от линии S образует в плоскости р ₁Op₂ ряд полос, происходящих, по Френелю, от различной разности хода лучей, которые распространяются от М и N к различным точкам около О.

В) Дифракционная оптическая сетка (reseau, Diffractionsgitter, grating) дает явления, имеющие особенный научный интерес. Сеткой называют стеклянную прозрачную пластинку с параллельными плоскими поверхностями, часть которой покрыта с одной стороны нарезанными алмазом черточками близко друг к другу (от 20 до 800 в 1 мм). Эти черточки обычно оказываются менее прозрачными, чем остальная часть поверхности. Первый Фраунгофер приготовил такую сетку, чтобы воспользоваться ею для получения спектров и измерения длины световых волн. На черт. 4 оптическая сетка представлена в разрезе .

Черт. 4.

A₁B₁=A₂B₂=A₃B₃...=a соответствуют ее прозрачным промежуткам, B₁A₂=B₂A₃=...= b — означают малопрозрачные матовые штрихи. Однородный свет (с длиной волны λ) от удаленной светящейся линии подходит к сетке в виде параллельных лучей SA₁, SB₁,...; следовательно, поверхность эфирных волн, приходящих к сетке, будет плоскость MN — параллельная поверхности сетки. По принципу Гюйгенса, каждая точка элементов A₁B₁, A₂B₂,... этой плоской волны является независимым центром для колебаний, распространяющихся по всем направлениям. Из чертежа видно, что должно существовать такое направление, наклонное к падающим лучам под углом α, следуя по которому, лучи попарно A₁ а ₁ и A₂ а ₂, A₂ а ₂ и A₃ а ₃... и т. д. отстанут друг от друга на одну волну. При таком условии лучи A₁ а ₁, A₂ а ₂ и A₃ а ₃ и т. д. будут друг друга усиливать и мы увидим отдаленную светящуюся линию по направлению, образующему угол α с падающими лучами, но менее яркой , чем по направлению падающих лучей SAS₁. Это будет дифракционным изображением S — первого порядка. Другая система лучей, еще более отклоненных от падающих лучей, но при условии, что лучи, подобные A₁ а ₁ и A₂ а ₂, будут отставать друг от друга уже не на одну волну, а на две волны, даст новое изображение линии S — еще более слабое — изображение второго порядка. Пучки лучей в промежуточных направлениях будут давать minima света и т. д. Все это можно выразить формулой, которую дает волнообразная теория света для яркости (J) лучей, идущих от отверстий сетки по какому-нибудь направлению, образующему угол θ с направлением падающих:

Maxima и minima яркостей J будут зависеть от maxima и minima значений функций P и Q. Теория доказывает, что J имеет три класса maxima, из которых, в случае малого размера ширины (а) прозрачных промежутков и большого числа (п) матовых штрихов, преобладающими (главными) остаются maxima II класса, так как с ними совпадают maxima I кл. Maxima же III кл., будучи чрезвычайно слабыми и располагаясь между maxima II кл. (следовательно, на месте minima II кл.), становятся в этих условиях вовсе незаметными. То, что мы назвали дифракционными изображениями 1-го, 2-го 3-го порядков — не что иное, как 1-й, 2-й, 3-й maxima II кл. Условными уравнениями для главных maxima будут:

Сумма (a + b) называется элементом сетки и измеряется в мм. Так как (a + b) мм можно выразить через 1/n мм, принимая за п число делений в 1 мм, то для общего случая — спектра т-го порядка

sin θ = т. nλ

откуда можно определить длину волны

зная (a + b), т и θ с помощью особого угломерного прибора (см. Спектрометр). Из уравнений видно, что для лучей с более короткой волной λ' < λ соответственные углы будут меньше и направления, по которым будут видны изображения светящейся линии S различных порядков для этого сорта лучей, будут ближе к нормали. Поэтому, если S посылает сложный белый свет, мы заметим через сетку ряд спектров, симметрично расположенных по сторонам центральной белой полосы. Красные лучи, сравнительно с фиолетовыми, будут более отклонены от нормали. Отклонения разных цветных лучей в дифракционном спектре пропорциональны длинам волн, в потому такие спектры, в отличие от призматичных, назыв. нормальными спектрами [Замечательно точные измерения длин волн в солнечном дифракционном спектре и первый атлас нормального спектра были исполнены в 60-х годах Энгстремом (Angström. "Recherches sur le spectre Solaire", Uppsala, 1868).].

При большом числе п в 1 мм фиолетовые края спектров высших порядков накладываются на красные концы спектров низшего порядка. На черт. 5 показано расположение дифракционных спектров около центральной белой полосы О.

Черт. 5.

Черт. 6 показывает разницу в общем характере солнечного спектра, полученного от сетки и от призмы при условии, что длина спектров между фраунгоферовыми линиями А (в красной части) и К (в фиолетовой) одна и та же.

Черт. 6.

Такие же явления, но еще более яркие, могут быть получены с отражательными сетками, т. е. с пластинками из зеркального металла, на которых алмазом нарезаны близко друг к другу матовые штрихи. Мы знаем, что от светящейся линии лучи, падающие на плоское зеркало, после отражения принимают такое направление, какое они имели бы, если бы выходили из светящейся линии, помещенной за зеркалом на том же расстоянии, на котором в действительности она находится перед зеркалом. Поэтому все рассуждения, сделанные относительно прозрачных сеток, вполне приложимы и к отражательным сеткам. В последние 16 лет стали пользоваться исключительно отражательными сетками.

Если на плоскую сетку лучи падают наклонно, под углом i, то, в случае спектра m- го порядка, условн. ур. будет

если θ обозначает угол между дифр. лучом и отраженным. Дифракционная сетка, подобно призме, может быть установлена на minimum отклонения θ, но для этого необходимо в написанном сейчас уравнении сделать

Дисперсией сетки называют

Она будет наименьшей при условии

i = —  θ, т. е. при условии, когда дифракционные лучи идут по нормали к сетке. Для раздвоения линии D в солнечном спектре 1-го порядка необходимо иметь на сетке, по крайней мере, 40 штрихов в 1 мм. Дисперсия в желтой части (D) спектра 1-го порядка от большой отражательной сетки Роуланда (20000 штрихов в 1 дюйме, на протяжении 5,5 дюймов — 110000 штрихов) равна дисперсии системы призм (с показателем преломления 1,65), в которой пройденный лучами путь равен 126 см (система заключает 60 призм, если длину луча, проходимого в каждой призме при minimum 'е отклонения, принять равной 2,1 см). В желтой части солнечного спектра 1-го порядка от большой сетки Роуланда можно видеть еще отдельными такие фраунгоферовы линии, которые различаются по длине волны только на 0,005 μμ (μ = микрону = 0,001 мм, μμ = 0,001 μ  = 0,000001 мм).

Вогнутой сеткой Роуланда (Rowland, 1882) называется сферическое вогнутое зеркало, на поверхности которого проведены алмазом черточки (длиной до 1¹/₂ дюймов, в числе или 10000 или 20000 штр. в 1 дюйме). Такая сетка обладает следующим замечательным свойством.

Черт. 7

Если на окружности, описанной около радиуса кривизны сетки, как около диаметра, (черт. 7) расположить щель S и фотографическую пластинку С (или окуляр), прикрепив их к концам стержней, вращающихся около оси О в плоскости круга, то, при определенном положении щели S существует такое положение пластинки С на окружности, при котором на ней получается совершенно резкий отчетливый спектр, "в фокусе". Если обозначить DS = d, DR = r, DC = f, угол падения лучей SDR = i, а угол BDC = 0, то теория доказывает, совершенно согласно опыту, что:

При практическом пользовании вогнутой сеткой берут θ = 0, след., cos θ = 1 и f = r, для всех частей спектров (см. Спектроскоп). Вогнутые сетки, приготовленные Роуландом на специально устроенной делительной машине [Для приготовления самой большой сетки Роуланда с 110000 делениями требуется от 3 до 4 суток непрерывной работы делительной машины. Температура сетки и винта должна поддерживаться, насколько возможно, постоянной. С этой целью делительная машина находится в особом помещении под землей и приводится в действие двигателем, установленным снаружи.], дали ему возможность сфотографировать с большими подробностями солнечный спектр, измерить длины волн с точностью до 0,01 μμ и приготовить фототипии для замечательного атласа солнечного спектра (1887), общая длина которого между 700 μμ и 300 μμ простирается до 12 м. Черт. 8 изображает группу линий в желтой части солнечного спектра около линий D₁D₂ и шкалу длин волн в десятимиллионных миллиметра (0,1 μμ) с негатива, полученного с одной из сеток Роуланда.

Черт. 8.

На оригинальных негативах Роуланда расстояние между линиями D₁ и D₂ равнялось 6 мм.

С) В предлагаемой таблице даны длины волн для самых главных линий солнечного спектра с указанием фамилии наблюдателя и элементов, от которых происходят линии. Длины волн для тепловых лучей получены Abney с помощью фотографии спектров от большой сетки Роуланда. Числа Роуланда взяты из его последнего сообщения: "Astronomy and Astrophysics", 12, p. 321, 1893).

D) В зрительных трубках происходят явления Д., мешающие рассматриванию близких одна к другой звезд. Пусть небольшое отверстие MN (радиуса Мт = R) закрыто объективом с главным фокусом в О. (черт. 1) и пусть из отдаленной точки S падает на объектив пучок параллельн. лучей (длины волны λ). Согласно наблюдениям Фраунгофера в центре экрана О при таких условиях должен получиться светлый кружок, окаймленный рядом светлых и темных колец, диаметры которых изменяются прямо пропорционально λ и обратно пропорционально R. Эри (Airy) указал первый на значение этих дифракционных явлений для теории оптических инструментов. На основании принципа Гюйгенса-Френеля он вывел формулу яркости освещения (J) в различных точках экрана АОВ и из условных уравнений для maxima и minima J получил следующие выражения для угловых радиусов центрального кружка и блестящих колец:

Таким образом, очевидно, что в случае 2-х светящихся точек S₁ и S₂ (двойная звезда) лучи, пройдя через объектив, должны образовать в фокусной плоскости два кружка с кольцами. Когда кружки не накладываются друг на друга, но только соприкасаются или непосредственно, или первыми светлыми кольцами, тогда наблюдатель вполне уверен в существовании перед объективом 2-х отдельных светил. На этом основании принимают, что при данном отверстии объектива возможно резко разлагать двойную звезду на составляющие тогда, когда угол зрения, под которым видна из центра отверстия объектива линия, соединяющая две звезды, равен двойному углу Д. (2 ω ₁), для первого светлого кольца.

Величина 1/(2 ω ₁) названа Фуко (Foucault) оптической способностью инструмента (pouvoir optique, Leistungsfähigkeit, resolwing power). При объективе с диафрагмой в 12 см две светящиеся точки будут казаться раздельными, когда соединяющая их линия видна под углом в 3 сек. В действительности этот угол может быть еще меньше, и в опытах Фуко он был только 1 сек. (см. Зрение, Микроскоп, Телескоп).

Е) Звуковая дифракция. Д. присуща всем волнам вообще (световым, тепловым, химическим, электрическим и звуковым), но при условии, чтобы размеры экранов и отверстий значительно превосходили длину волн, но не обратно. Круглые экран и отверстие в 2 см диаметром, которые для световых, тепловых и химических — коротких эфирных — волн слишком велики (в 1000000 раз), для электрических эфирных волн Герца будут уже малыми (в 30 раз меньше [Недавно Риги (Righi) удалось наблюдать явления Д. со щелью шириной в 60 см для электрических коротких волн 20 см и 7 см (см. "La Lumière Electrique", 1, Juillet 93).], также будут они малыми и сравнительно с длиной воздушных, звуковых, волн, соответствующих тонам среднего регистра. Этим обстоятельством и объясняется, почему при обычных условиях не удавалось заметить ни звуковой тени, ни звуковой Д. Для опытов этого рода надо или взять экран и отверстие очень больших размеров, или воспользоваться очень высокими звуками (с короткими волнами). Недавно Райле (Rayleigh) воспользовался для подобных опытов свистком Гальтона, дающим такие короткие волны, которые даже не ощущаются органом слуха, но могут быть открыты по дрожанию газового пламени, особенным образом приспособленного (см. Пламя чувствительное). Райле доказал, что при звуковых волнах в 1-2 см длины можно наблюдать звуковую Д. с круглыми отверстиями и экранами в 15-20 см диаметром, при расстояниях от них свистка и чувствительного пламени в 75-100 см ("Nature" Лонд., V, 38 р. 208). Подробную литературу по Д. можно найти в курсах оптики — V erdet, Verdet-Exner, Mascart.