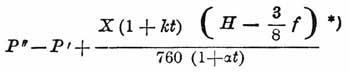
| [ начало ] | [ И ] |
Измерение газов
— При обыкновенных определениях количества газов измеряют объем, занимаемый газом в стеклянном сосуде, обыкновенно разделенном на куб. сантиметры при 15°С, температуру газа и его давление; затем, имея по таблицам вес одного кубич. сантиметра данного газа при наблюдаемых температуре и давлении, находят вес газа по формуле: вес тела в пустоте равен (в метрической мере) произведению из его объема на плотность (или вес единицы объема). Но под плотностью газа обыкновенно разумеют отношение веса газа к весу равного объема воздуха, взятых при нормальных условиях, т. е. при температуре 0°С и давлении 760 мм. Заметим, что для идеального газа, следующего закону Бойля-Мариотта, каковым и считается при обыкновенных определениях всякий газ, достаточно удаленный от сжижения; это отношение не изменится и при иной температуре и ином давлении. Очевидно далее, что для получения веса одного куб. см данного газа, нужно его плотность (по отношению к воздуху) помножить на вес одного куб. см воздуха. Точное определение плотности газа и веса одного куб. см воздуха, равно как и непосредственное взвешивание газа, выходят из ряда обычных определений, так как для таких определений необходимо иметь большие количества газа и весы, допускающие наивысшую степень точности взвешивания (см. Весы). О точности И. газов подробные данные имеются в отчетах проф. Менделеева: "Об упругости газов" (1875 г.) и "О весе литра воздуха" ("Временник главной палаты мер и весов", 1894 г.). Определения Реньо плотности газов и веса куб. см воздуха до сих пор считаются образцовыми; так, наприм., новейшим определениям веса куб. см воздуха Жолли, Ледюка и лорда Рэлея приходится придать одинаковый вес с Реньовскими. По расчетам Д. Менделеева ("Вр. Гл. П. М. и В."), средняя наивероятнейшая величина для веса куб. см сухого воздуха, лишенного углекислоты:
l0 = 0,131844g г ± 0,00010 г, где g — ускорение силы тяжести; для широты СПб. l0 = 1,29455 ± 0,000010 г.
Способ Реньо для определения плотности газов состоит в следующем: из нескольких стеклянных шаров емкостью около 10 литров, приготовленных на одном и том же заводе при одинаковых условиях, были выбраны два наиболее близкие по емкости; к ним на мастике были приделаны одинаковые арматуры с кранами. Прежде всего уравнивался наружный объем шаров таким образом: оба шара наполнялись водой, затем подвешивались на двух плечах точных весов и, по приведении весов в равновесие, погружались в общую ванну с водой. Вследствие неполного равенства наружных объемов, равновесие весов, конечно, нарушалось, для восстановления которого на одну сторону весов приходилось добавить некоторый груз р. Далее подбирался такой стеклянный грузик, который терял в воде как раз p г. Этот добавочный грузик Реньо подвешивал к меньшему шару, вновь уравновешивал шары в воздухе и потом снова погружал оба шара в воду, и так как равновесие не нарушалось, то этим и констатировалось полное равенство наружных объемов обоих шаров. Таким способом Реньо исключил большую поправку на потерю веса шаров в воздухе, которая зависела бы от изменения температуры, давления и влажности воздуха того помещения, где производились взвешивания; и действительно, равновесие весов с пустыми (без воздуха) запертыми шарами не нарушалось в течение многих дней. Потом один из шаров помещался в ванну с тающим льдом, на арматуру шара навинчивалась трубка с трехходовым краном и двумя трубками, из которых одна вела к дифференциальному барометру, другая шла к другому трехходовому крану, который сообщал внутренность стеклянного шара или с разрежающим насосом, или с резервуаром, содержащим сухой газ. Разрежая газ внутри шара и вновь наполняя шар газом из резервуара при помощи второго трехходового крана, до тех пор, пока не было уверенности, что остатки воздуха были удалены, Реньо производил в последний раз сильное разрежение, разобщал стеклянный шар при помощи второго тройного крана с насосом, отсчитывал разность уровней в дифференциальном барометре; потом запирал кран, находящийся в горле стеклянного шара. Таким образом, шар в момент запирания крана содержал объем V0 разреженного газа при 0° и давлении h. Затем добавочные части отвинчивались, и шар с разреженным газом подвешивался по-прежнему на весах. По прошествии некоторого времени температуры обоих шаров сравнивалась, объемы их также, некоторый добавочный груз на стороне шара с разреженным газом восстанавливал равновесие весов. Потом Реньо брал тот же шар, помещал его опять в ванну с тающим льдом и, при помощи добавочных частей, наполнял шар газом уже при давлении H, равном давлению атмосферы; когда температуру можно было считать установившейся, кран в горле шара закрывался и добавочные части отнимались. Очевидно, что в этот раз в шар был введен объем газа V0 при 0° и давлении H — h. При новом взвешивании на весах пришлось снять P г; очевидно, это и есть вес газа, введенного при втором опыте. По Мариоттову закону следует, что вес газа при том же объеме, но при 760 мм давления, будет P[760/(H — h)]. Ввиду того, что Н близко к 760 и h очень мало, конечно, нельзя ждать заметных отступлений в сжатии газа от Мариоттова закона. Подобным же образом Реньо получил вес воздуха, заключенного в объеме V0 при 0° и давлении 760 мм равным P'[760/(H' — h')]; искомая плотность газа, таким образом, равна
Δ = (P/P')[(H' — h')/(H — h)].
Приводим плотности, полученные Реньо для некоторых газов:
| Воздух | 1 |
| Кислород | 1,10563 |
| Водород | 0,06926 |
| Азот | 0,97137 |
| Углекислота | 1,52901 |
Определение веса куб. сантиметра воздуха, при 0° и 760 мм давления, Реньо произвел таким образом. По только что изложенному способу — Реньо определил вес воздуха, заключенного в стеклянном шаре при 0° в 760 мм
Х = Р[760/(H — h)];
остается лишь описать способ измерения емкости шара при 0°. Сначала взвешивался шар с открытым краном; вес гирь его уравновешивающих был Р'. Потом, навинтив на арматуру шара трубку, загнутую наподобие сифона, и введя внутрь шара некоторое количество воды и выкачивая пары воды вместе с воздухом, можно было заполнить весь шар водой, не содержащей воздуха. Затем шар с сифоном и сосудом охлаждался от 13 до 18 часов до нуля в ледяной ванне. После того кран закрывался, а добавочные части отвинчивались, шар же с водой подвешивался на весах. Так как в том помещении, где происходило взвешивание, температура воздуха держалась ниже 9°, а вода, как известно, сжимается, начиная от 0 до + 4° и затем, снова расширяясь, достигает лишь при + 9° того же объема, то, очевидно, шар Реньо, заполненный водой при 0, не мог лопнуть от расширения воды. Вес шара с водой был Р"; тогда истинный вес воды, заключенной в шаре, равен:
[Реньо не делал поправок на потерю веса гирями в воздухе.]. В этой формуле k — коэффициент расширения стекла, α — коэффициент расширения воздуха, H, t и f — давление, температура и упругость паров воды в том помещении, где происходило взвешивание. Формула выражает, что истинный вес тела равен кажущемуся Р" — Р' + потеря веса тела в воздухе (см. Взвешивание). После того, как истинный вес воды найден, нужно этот вес разделить на плотность воды при нуле; частное и будет емкость шара в кубич. см = V0, а вес кубич. Сантиметра воздуха будет равен
α = X/V0.
Таким образом, для лаборатории Collège de France, находящейся на высоте 60 м над уровнем моря и в широте 48°50'14", литр воздуха весит, по Реньо, 1,29320 г. Теперь остается лишь привести обычный способ определения емкости сосуда взвешиванием. Емкость сосуда поверяется или измеряется обыкновенно таким образом: берут какой-нибудь сосуд с водою или ртутью, взвешивают его и выливают воду или ртуть в измеряемый сосуд до черты; по разности определяют вес вылитой жидкости. Если жидкость имеет на воздухе вес μ и плотность ее ς, то объем ее равен
v = μ / ς (1 + λ / ς — λ / δ) куб. см
где λ — вес кубич. см воздуха и приблизительно равен = 0,0012 г, δ — плотность разновесок (для латуни δ = 8,4). Для воды и латунных разновесок, при t = 15°, λ / ς — λ / δ = 0,00106. Вес куб. см воздуха при любой температуре t и давлении H выражается формулой
l = [0,001293Н]/[(1 + 0 ,00367t)760].
О приемах отчета объемов газов в стеклянных трубках см. Мениск (подробности см. у Бунзена: "Gasometrische Methoden").
Н. Смирнов. Δ.