| [ начало ] | [ К ] |
Катоптрика
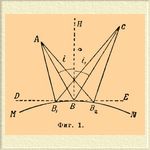
(κατά — внутри, ϋπτομαι — видеть) — часть оптики, излагающая законы отражения света от зеркальных поверхностей и применение этих законов к устройству оптических инструментов. Когда световая волна идет из одной среды в другую (см. Диоптрика, Свет) и скорость света в этих двух средах неодинакова, то на поверхности их раздела образуются две системы волн — одна преломленная, продолжающая свой путь в среде второй, другая отраженная, продолжающая свой путь в первой среде. К. исследует законы распространения отраженных волн, пользуясь для этого общим упрощающим приемом геометрической оптики — именно заменой рассмотрения волн (сферических) рассмотрением их радиусов — или световых лучей. Отражение света от поверхностей в зависимости от природы поверхности бывает двух родов: 1) правильное, зеркальное, происходящее от свободной поверхности жидкостей и от блестящих полированных поверхностей стекла, металла, камней и т. д. (см. Зеркало); подобное отражение характеризуется тем, что каждый точно ограниченный пучок лучей дает при отражении тоже только один, точно ограниченный пучок, направленный в одном точно определенном направлении; 2) рассеянное, диффузное — от шероховатых поверхностей, дающих от падающего пучка целый ряд световых лучей, расходящихся по всевозможным направлениям. Обыкновенно вследствие несовершенств полировки даже при зеркальных поверхностях отраженный свет осложняется рассеянным светом; чем совершеннее полировка, тем рассеянного света меньше [Нет определенного предела шероховатости, при котором диффузное отражение переходит в зеркальное. В оптике доказывается, что для зеркального отражения необходимо, чтобы величина 2hcosi, где h вышина неровностей на поверхности, а i угол, под которым свет падает на поверхность, составляла всего малую долю длины световой волны, которая и сама чрезвычайно мала. При значительном наклоне (i велико, cosi мал) даже при большом h, величина 2 h cosi сделается весьма малой, т. е. может получиться зеркальное отражение от шероховатых поверхностей (отражение изображения свечи, окна от гладкой бумаги).]. О причинах появления рассеянного света см. Свет. К. занимается исключительно изучением законов правильного отражения [Притом от поверхностей достаточной величины; отражение от весьма малых поверхностей искажается явлением дифракции (см.)], не входя притом в рассмотрение тех особенных свойств светового луча (поляризация, окрашивание), которые он может получить при отражении. Та часть светового луча, которая лежит между источником и поверхностью раздела сред, назыв. падающим лучом, дальнейшая часть луча — отраженным. Падающий и отраженный лучи связаны следующими законами (фиг. 1):
Фиг. 1
1) Каждый падающий луч AB дает всего один отраженный луч ВС. 2) Если в точке падения луча проведем к отражающей поверхности (MN) касательную плоскость DBE, а к последней в точке падения — перпендикуляр ВН, то падающий луч, перпендикуляр и отраженный луч лежат в одной плоскости. 3) Угол, образованный падающим лучом с перпендикуляром BH, — угол i, называемый углом падения, — равен углу, образованному отраженным лучом с тем же перпендикуляром — углу i', называемому углом отражения. Все эти положения объединяются в одном законе, высказанном Ферматом, что между двумя данными точками на падающем и отраженном луче путь света есть кратчайший, т. е. что путь ABC, обусловленный вышесказанными законами, короче всякого другого возможного пути АВ 1 С, AB 2C и т. д. При отражении света от поверхности, отделяющей одну среду от другой, оптически более плотной (отражение идущих в воздухе лучей от стекла, жидкостей, металлов), всегда отражается лишь часть света, остальная преломляется; при отражении же света от поверхности менее плотной среды возможен случай полного (внутреннего) отражения (см. Диоптрика [О количестве отраженного света см. Свет.]). Расходящийся пучок света, заключенный между двумя крайними лучами AB, АВ 1, идущими из той же точки А и наклоненными друг к другу под углом α, смотря по форме отражающей поверхности и расстоянию от нее точки А, образует отраженный пучок света, который может быть либо тоже расходящимся, притом в случае плоской поверхности с тем же углом расхождения (фиг. 2; α ' = α), а при отражении от кривой поверхности — расходящимся (фиг. 2 и 3) или сходящимся (фиг. 3).
Фиг. 2.
Фиг. 3.
В случае, если отраженный пучок расходящийся, наблюдателю источник света кажется лежащим за отражающей поверхностью в точке пересечения А' продолжений отраженных лучей. Эта мнимая точка исхождения лучей А назыв. мнимым, или кажущимся, изображением точки фиг. 3 и 4. В случае образования сходящегося пучка лучей — точка пересечения лучей А' дает перед зеркалом действительное изображение точки А (фиг. 4).
Фиг. 4.
Если вместо точки А будет предмет, представляющий совокупность множества точек, излучающих собственный или отраженный свет, то получится от каждой точки предмета мнимое или действительное зеркальное изображение; совокупность этих изображений дает мнимое или действительное зеркальное изображение предмета. О свойствах симметрии зеркальных изображений см. Зеркало.
Плоские зеркала. Простейший случай отражения представляет отражение от плоского зеркала. Мнимое изображение точки А (фиг. 2) получается в А' на расстоянии от зеркала MN равном А'К = АК, и в этом случае α ' = α. Совокупность точек, представляющих предмет AB, дает за зеркалом мнимое изображение его ab (фиг. 5), равное предмету по величине и расстояние точек которого от зеркала равно расстоянию соответствующих точек предмета от зеркала.
Фиг. 5.
Поэтому человек, смотрящий в зеркало, увидит свое изображение за зеркалом на таком расстоянии от него, на каком он сам находится перед зеркалом, т. е. зеркало всегда будет находиться на полпути между человеком и его мнимым изображением [На этом основан способ определения толщины стекла в зеркалах. К зеркалу приставляют заостренную палочку (карандаш) и определяют на глаз расстояние l между концом карандаша и его изображением. Половина l, умноженная на коэффициент преломления стекла (1,5), т. е. l/2 x 1,5 = 3/4l, дает толщину стекла.]; отсюда ясно, что зеркало должно иметь половину роста человека для того, чтобы он мог всего себя в нем видеть. Если поворачивать зеркало вокруг оси параллельной его плоскости, то угол падения луча, направленного на зеркало, а следовательно, и угол отражения его изменятся, причем если зеркало отклонить на угол α, то отраженный луч отклонится на угол 2α. На этом основан способ так называемого зеркального отчета, служащий для наблюдения и измерения весьма небольших угловых поворотов.
Фиг. 6.
Пусть имеется свободное вращающееся вокруг какой-либо оси тело (фигура 6; на ней ось перпендикулярна бумаге и пересекает ее в точке а); прикрепим к телу зеркало ST, вращающееся вместе с телом, и установим на некотором расстоянии l от зеркала зрительную трубу, посредством которой наблюдаем мнимое изображение в зеркале шкалы MN, расположенной под трубой, перпендикулярно к оси вращения а; при положении зеркала ST мы видим в трубе деление о шкалы; при повороте предмета, а с ним и зеркала, в положение S'T', на угол α, мы увидим в трубе уже x-ое деление шкалы, так как теперь луч xa, идущий от него, отразившись от S'Т, попадет в трубу; находим угол α из зависимости:
tang 2 α = x/l (1)
Если, например, l = 2 м, х = 1 см, то α = 17 секундам (угл.). Этот весьма чувствительный способ (Гаусса и Поггендорфа) отсчета особенно часто применяется для наблюдения небольших поворотов магнитных стрелок в гальванометрах (см.). На подобном же принципе основан целый ряд угломерных приборов, как то: секстант (см.), гониометр (см.) и т. д., также гелиостаты и тому подобные приборы. Мнимое изображение одного зеркала по отношению к другому зеркалу играет роль действительного изображения; поэтому изображение одного зеркала в другом получается с передачей всех мнимых изображений первого. Это дает объяснение явлениям, происходящим в наклоненных друг к другу зеркалах. Если два зеркала P и Q наклонены друг к другу под углом φ и между ними помещена светящаяся точка L, то вообще увидим внутри зеркал целый ряд изображений светящейся точки, расположенных по кругу, по окружности которого находится и светящаяся точка L; число их увеличивается с уменьшением угла φ. Это объясняется тем, что мнимые изображения L в двух зеркалах, отражаясь от противоположных зеркал, дают пару новых изображений, которые, в свою очередь, вызывают новые изображения и т. д. Бертен показал, что число N этих изображений, лежащих по окружности круга, лежит между пределами (2π / φ + 1) и (2π / φ — 1). Если угловое расстояние предмета L от одного зеркала P есть θ, следовательно, от другого (Q) φ — θ, то полное число изображений состоит из совокупности двух рядов изображений, составляющих с зеркалами углы θ, (θ + φ), (θ + 2 φ)... и (φ — θ), (2 φ — θ), (3 φ — θ)... и т. д. Одни из этих изображений (полученные некратным числом отражений) представляются симметричными, но не налагающимися на предмет, другие (полученные кратным числом отражений) налагающимися [Т. е. такими, которые одним движением или вращением вокруг оси, параллельной ребру зеркал, можно привести в совпадение с предметом L. ] на него. На многократном отражении между наклоненными зеркалами основан калейдоскоп (см.). Если φ = 0, т. е. зеркала P и Q параллельны, то число изображений теоретически бесконечно. В обыденной жизни (см. Зеркало) применяют обыкновенно прозрачные стеклянные зеркала, крытые металлическим, отражающим свет слоем с задней стороны, поэтому луч раньше, чем достигнуть отражающей поверхности, должен пройти через слой стекла и, отразившись, снова пройти через тот же слой (фиг. 7).
Фиг. 7.
При этом весьма малая часть света АтО отражается прямо от передней поверхности стекла и дает свое слабое мнимое изображение а; часть же света, отраженного от задней поверхности, попадает на переднюю, отражается от нее на заднюю и дает, пройдя путь AstqxyO, свое изображение а 2 и т. д. Главное изображение а получается от луча АnprО, дважды преломленного и раз отразившего. Слабые изображения а, a2 и т. д. едва заметны при малых углах падения, но становятся весьма заметными при больших углах. Поэтому в измерительных и научных приборах применяют обыкновенно зеркала с отражающею поверхностью — в прежнее время металлические, теперь стеклянные посеребренные — или призмы с полным внутренним отражением (см. Призма).
Сферические зеркала. При отражении от кривых поверхностей расходящийся пучок света, отразившись, может дать либо тоже расходящийся пучок (фиг. 3), в каком случае изображение получается мнимое, либо сходящийся (фиг. 4), в каком случае оно получается действительным. Можно поставить себе задачу — определить свойства поверхности, отразившись от которой, лучи дадут одно правильное, действительное или мнимое, изображение источника света; такая поверхность называется апланатической. Математический анализ вопроса выясняет, что этому условию для действительных изображений удовлетворяет поверхность эллипсоида вращения вокруг большей оси; если в одном фокусе его поместить светящуюся точку, то отраженные лучи пересекутся все в другом фокусе. Если источник света находится весьма далеко, то условию апланатизма удовлетворяет параболоид. Но так как поверхность шара легче всего выполнить технически, то в К. довольствуются рассмотрением свойств сферических зеркал. Отражающая поверхность шара называется выпуклым зеркалом, если выпуклость его направлена к источнику света, и вогнутым, если к источнику направлена вогнутость. Точка S (фиг. 8) пересечения зеркала линией, соединяющей центр его с источником, назыв. вершиною зеркала; линия же эта, на которой лежит обыкновенно и изображение, называется главною осью зеркала.
Фиг. 8.
Угол, под которым из центра шаровой поверхности видно само зеркало, называется его угловым отверстием (MCN), диаметр зеркала тоже иногда называют его (линейным) отверстием. Зеркала с небольшим отверстием (10-15°) с достаточною точностью апланатичны. Если источник находится в таком большом расстоянии, что лучи, идущие от какой-либо точки его, близко параллельны между собою, то, отразившись от такого зеркала, от разных точек его (фиг. 8), они пересекутся в одной точке F, называемой главным фокусом зеркала, и дадут в случае вогнутого зеркала — действительное, в случае выпуклого — мнимое изображение предмета, лежащее на расстоянии от центра кривизны CF, равном r/2, где r — радиус шаровой поверхности. Если светящуюся точку от бесконечности будем приближать к вогнутому зеркалу, то изображение ее будет перемещаться вдоль главной оси, приближаясь к центру кривизны зеркала С, и наконец совпадет с этим центром, когда и светящийся предмет будет в центре зеркала, т. е. тогда предмет и его изображение совпадут. По мере того, как точка, приближаясь к зеркалу, будет перемещаться от С к F, изображение будет удаляться от С, и наконец, когда точка придет в F, изображение ее уйдет по оптической оси бесконечно далеко. Приближая точку еще больше, заметим, что теперь лучи отражаются уже расходящимся пучком, следовательно, дают мнимое изображение, которое по мере приближения предмета от F к вершине быстро приближается от бесконечности тоже к вершине. Во всех положениях точки L она связана так с положением своего изображения J, что, поместив точку в L, мы получим изображение в J, поместив же точку в J — изображение получим в L; по причине этих свойств эти две точки называют сопряженными фокусами. Положение этих точек по отношению к зеркалу определяется выражением
1/d + 1/f = 2/r = 1/F
где F — расстояние главного фокуса от вершины зеркала, d и f — расстояния от той же точки источника света и его изображения.
при 1) d= ∞..... f = r/2 действительное изображение
2) d > r......... r/2 < f < r действительное изображение
3) d = r...... f = r действительное изображение
4) r/2 < d < r...... f > r действительное изображение
5) d = r/2........ f = ∞
6) 0 < d < r/2; f — мнимое изобр.
В первых четырех случаях изображение получается действительным пересечением лучей: если в место пересечения лучей поставим экран, то на нем получим изображение светящейся точки; в случае 5-м изображение находится бесконечно далеко или практически вовсе не образуется; в 6 случае изображение мнимое. Если источником света служит предмет S, то в сопряженном его фокусе получается изображение его (фиг. 9);
Фиг. 9.
в первых четырех случаях оно действительное и опрокинутое, а в шестом (фиг. 10) — мнимое и прямое.
Фиг. 10.
Величина изображения Y
при 1) d > r.....Y < S Действительное изображение
2) d = r..... Y = S Действительное изображение
3) r/2 < d < r ..... Y < S Действительное изображение
4) d = r/2....Y = ∞ Мнимое изображение
5) 0 < d < r/2.... Y > S Мнимое изображение
6) d = 0..... Y = S Мнимое изображение
Величина изображения солнца в зеркале с радиусом R будет = 0,0045 R = 0,009F. Если F = 5 метрам, то величина изображения солнца = 45 млн. Если светящаяся точка находится не на главной оптической оси, а на некоторой побочной, то изображение получается на другой побочной оси, сопряженной с первой и образующей с главною осью такой же угол, как и первая. Выпуклые зеркала от расходящегося пучка света дают исключительно мнимые изображения.
Фиг. 11.
Главный мнимый фокус их (фиг. 11) — место схождения продолжений лучей, отраженных от зеркала, если источник света находится на главной оси бесконечно далеко — лежит за зеркалом на расстоянии от него равном r/2. По мере приближения точки от бесконечности к зеркалу мнимое изображение ее перемещается от главного фокуса F к зеркалу. В выпуклых зеркалах зависимость между d, f и F дается выражением
1/f — 1/d = 2/r = 1/F
откуда и следует, что при
1) d = ∞.......f = r/2
2) 0 < d < ∞... f < r/2
3) d = 0.......f = 0
Если источником света служит предмет, то во всех случаях выпуклое зеркало дает мнимое прямое изображение его; величина изображения будет всегда меньше предмета L. Ньютон дал очень простую формулу, связывающую величины f, d и F для всякого сферического зеркала. Если считать f и d не от вершины зеркала, а от точки F, то расстояния fF и dF связаны будут равенством
fF ∙ dF = F2
Если в этом равенстве считать направления по одну сторону фокуса за положительные, а по другую за отрицательные, то оно может дать нам положение сопряженных фокусов в выпуклом и вогнутом зеркалах. На свойствах вогнутых зеркал основано устройство катоптрических телескопов, или рефлекторов.
Сферическая аберрация. Сферические зеркала лишь приблизительно апланатичны. Если светящаяся точка находится в бесконечности, то для некоторого пучка, составляющего с радиусом угол i, F = не r/2, как бы следовало по формуле, а равно
| i = 1° | 0,49994r |
| i = 2° | 0,49969r |
| i = 5° | 0,49809r |
| i = 10° | 0,49229r |
| i = 15° | 0,48236r |
| i = 20° | 0,45552r |
Вообще для некоторого угла i расстояние фокуса от вершины равно F = r∙(Sini/Sin2i)
Лучи пересекаются на главной оси так, что точка пересечения краевых лучей будет лежать ближе к вершине, чем точка пересечения центральных. Явление это называется сферической аберрацией зеркала. Пересечение лучей образует поверхность, назыв. каустическою поверхностью (см. Зажигательные кривые). На фиг. 12 изображен разрез половины каустической поверхности вогнутого зеркала.
Фиг. 12.
Форма каустической поверхности зависит от расстояния светящейся точки; если светящаяся точка лежит бесконечно далеко, то каустическая поверхность называется главною. Если пересечь главную каустическую поверхность плоскостью, перпендикулярною к оси и проходящею через фокус центральных лучей, то получим в сечении кружок, радиус которого S называется главною поперечною аберрацией. Расстояние по оси λ между фокусами крайних краевых и центральных лучей называется главною продольною аберрацией. Величины ρ и λ определяются следующими выражениями:
Ρ = R3/2r2 и λ = R2/4r
где R — радиус отверстия зеркала, а r — радиус кривизны. Каустическая поверхность имеет наиболее узкое сечение в точке, отстоящей от фокуса центральных лучей на расстоянии 3/4 λ; в этом месте радиус сечения ее равен 1/4 λ. Другим следствием сферической аберрации является искривление изображения; изображение удаленных плоских предметов представляется выпуклым и обращенным выпуклостью к зеркалу; изображение предметов, находящихся в центре, вполне правильно; изображение предметов, находящихся между центром и зеркалом, обращено к зеркалу своею вогнутостью. Аберрация делает невозможным получение точных изображений с помощью сферических зеркал, и поэтому в приборах, в которых требуется достижение вполне правильных изображений (рефлекторы, прожекторы), пользуются параболическими зеркалами. Для этой цели зеркала шлифуются сначала сферическими, а затем от руки придают зеркалам параболическую форму, отшлифовывая края сильнее центра [Чтобы перейти от сферы к параболоиду, достаточно, даже у больших зеркал, снять с краев стекла слой чрезвычайной тонкости; так, напр., в большом зеркале лорда Рооса (R = 1646 см, D = 45,5 см) толщина снятого на краях слоя равнялась 1/400 мм]. Другой (менее совершенный) способ исключения сферической аберрации, придуманный полк. Манженом, применяется в прожекторах (см.): в них зеркало представляет двояковогнутую чечевицу, посеребренную на задней стороне (фиг. 13).
Фиг. 1 3.
Кривизны поверхностей выбраны так, что крайние лучи, преломившись дважды через большую толщу стекла, пересекутся в той же точке что и центральные лучи.
Цилиндрические и конические зеркала. Цилиндрические и конические зеркала (выпуклые и вогнутые) дают искаженные изображения предметов; наоборот, можно приготовить искаженные рисунки предметов, которые, будучи рассматриваемы в цилиндрическом или коническом зеркале определенной кривизны, дадут впечатление правильного рисунка. Такие рисунки называются анаморфозами.
История К. Равенство углов падения и отражения, по свидетельству Плутарха, известно было еще философам школы Платона (329-447). Определенно высказал его только Евклид (330 д. Р. Х.) в своей "Катоптрике" (издана в первый раз в Париже, 1557); в этом же сочинении встречается впервые точное разграничение явлений преломления (διάκλασις) и отражения (κάτακλασις). Более общий принцип кратчайшего оптического пути был высказан позже Героном Александрийским (150 д. Р. Х.), затем Ферматом (1601-1665) и Мопертюи (1698-1759). Вопрос об отражении между зеркалами под углом вполне разрешен был лишь недавно Бертеном (1850); изобретение калейдоскопа Брюстером относится к 1818 году. Явления отражения от кривых зеркал были известны еще, быть может, в глубокой древности. В первые дни Рима Нума (714-671) будто бы пользовался зажигательным зеркалом для зажигания огня Весты. По свидетельству Цецеса (византийский историк XII стол.), Архимед (287-212 до Р. Х.) будто бы вогнутым зеркалом зажег флот Марцелла, а по свидетельству Зонара, неоплатоник Прокл (412-485) тем же способом зажег у Константинополя флот Виталина. Вопрос о зажигательных свойствах зеркал пользовался в средние века большою популярностью — им занимались Шотт, Кирхер и затем позже Бюффон (1707-1788). На положение главного фокуса у зеркал впервые указал Рожер Бакон (1214-1294) в "Opus rnajus" (1267), но верное его положение показал Порта (1058). Основное уравнение зеркал df = F2 дано было Ньютоном в 1764 г. в его "Optica". На существование сферической аберрации указывал еще Декарт (1596-1650), на каустическую поверхность Чирнгауз (1682). Подробнее изучали свойства каустиков Делагир (1060) и Ив. Бернулли (1692); вопрос этот, представляющий большой математический интерес, изучали позже Малюс(1811), Жергон и Левисталь. Когда Цучи (1616), Мерсенн (1844), Грегори (1663), Ньютон (1668) и др. начали применять вогнутые зеркала к телескопам, то явились попытки уничтожить влияние сферической аберрации. Кассегрен (1675) старался уничтожить его, комбинируя вогнутое зеркало с выпуклым, имеющим противоположную аберрацию. Еще в 530 г. Антемий указывал на апланатичность эллипсоидальных зеркал; позже Бакон советовал придать зеркалам форму параболоидов. Первая попытка выполнить это была сделана Мэджем (1777), но лишь знаменитый Фуко (в 1857-1859 г.) выработал правильную техническую систему придавания зеркалам параболоидальной формы. Подробнее К. и ее литературу см. Verdet, "Le ç ons d'Optiique"; Mascart, "Traite d'Optique" и др.
А. Гершун.
|
Page was updated:Tuesday, 11-Sep-2012 18:15:31 MSK |