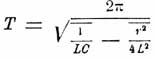
| [ начало ] | [ К ] |
Колебательный разряд
— При разряде какого-либо наэлектризованного тела, конденсатора, лейденской банки или батареи, состоящей из нескольких таких банок, электрический ток, являющийся в проводнике, при посредстве которого производится разряд, имеет вполне определенное направление и данный электрический заряд исчезает весьма быстро только тогда, когда сопротивление этого проводника очень большое. Совсем не то наблюдается в том случае, когда исследуемый разряд происходит через проводник, имеющий вообще небольшое сопротивление. В этом случае в проводнике возникает ряд быстро следующих друг за другом электрических токов противоположного направления, а само тело, конденсатор или батарея лейденских банок, прежде чем потерять свой заряд, несколько раз перезаряжаются противоположными электричествами. Получающиеся при этом заряды мало-помалу уменьшаются и периодически изменяющаяся числовая величина электрического потенциала на теле, или периодически изменяющаяся числовая величина разности электрических потенциалов поверхностей конденсатора постепенно приближается к нулю. Такой разряд называется колебательным. Причина возникновения К. разряда заключается в самоиндукции проводника (см. Самоиндукция). В. Томсон (ныне лорд Кельвин) впервые, на основании теории, указал необходимость существования таких К. разрядов и вывел формулу, по которой может быть вычислена величина периода полного электрического колебания, т. е. продолжительность одного полного изменения заряда данного тела или данного конденсатора. Эта формула:
Здесь T обозначает период полного электрического колебания, C обозначает электроемкость данного наэлектризованного тела или конденсатора, r обозначает сопротивление проводника, через который происходит разряд, a L обозначает коэффициент самоиндукции этого проводника. Величина заряда, появляющегося в теле или в конденсаторе при К. разряде, спустя t секунд после момента начала последнего, выражается, согласно теории Томсона, формулой
в которой Q0
обозначает первоначальный заряд, a ε обозначает
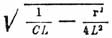 .
Когда проводник, через который происходит разряд, имеет очень малое
сопротивление, т. е. когда можно пренебречь величиной r2/4L2
в сравнении с величиной 1/ LC
, период полного электрического колебания выражается через
.
Когда проводник, через который происходит разряд, имеет очень малое
сопротивление, т. е. когда можно пренебречь величиной r2/4L2
в сравнении с величиной 1/ LC
, период полного электрического колебания выражается через
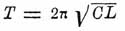 .
.
Правильность теоретических выводов Томсона подтверждается многочисленными наблюдениями явлений разряда. Такие наблюдения, первые по времени и наглядно обнаружившие все особенности К. разрядов, принадлежат Феддерсену, который изучал характер разряда лейденских банок по способу, употребленному ранее Витстоном. Он наблюдал получавшуюся при разряде электрическую искру при посредстве зеркала, быстро вращавшегося около оси, параллельной искре. Изображения искры, являвшейся при разряде лейденской банки или батареи из нескольких банок через проводник не очень большого сопротивления, представлялись всегда в виде полоски, состоявшей из отдельных, следующих друг за другом светлых и темных частей. Измерив угловое расстояние между двумя одинаковыми светлыми частями изображения искры и зная скорость вращения зеркала, Феддерсен мог вычислить период наблюдаемых электрических колебаний. Опыты Феддерсена показывают, что периоды электрических колебаний, возбуждающихся при разряде лейденских банок, выражаются в стотысячных долях секунды. Но периоды электрических колебаний могут быть получены много меньшими. Для этого достаточно вместо разряда лейденской банки произвести разряд тела, у которого электроемкость меньше, чем электроемкость лейденской банки. В опытах Герца (см. Герца опыты) получались К. разряды с периодами, выражающимися в стомиллионных и даже еще в более малых долях секунды. Явление молнии представляет собой также К. разряд, вследствие чего удар в какой-либо проводящий предмет, например, в громоотвод, сопровождается возникновением в этом предмете ряда быстро изменяющихся, как по силе, так и по направлению, электрических токов. Поэтому-то громоотводы должны быть устроены так, чтобы они без вреда для себя могли быть хорошими проводниками таких быстро изменяющихся токов (см. Громоотвод и Электрический ток).
И. Боргман.
|
Page was updated:Tuesday, 11-Sep-2012 18:15:37 MSK |