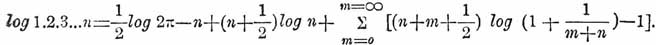
| [ начало ] | [ К ] |
Комбинаторный анализ
— математическая теория, занимающаяся определением числа различных способов распределения данных предметов в известном порядке; имеет особенно важное значение в теории уравнений и в теории вероятностей. Простейшие задачи этого рода заключаются в определении числа: размещений, сочетаний и перестановок.
Размещениями m предметов по n называются группы, которые можно составить из m предметов таким образом, чтобы каждая группа заключала в себе n предметов и все такие группы отличались бы одна от другой — или предметами в них входящими, или порядком распределения предметов. Число всех возможных размещений, какие можно составить из m предметов по n обозначается символом Anm и доказывается, что Апт = m(m—1)(m—2)(m—3)...(m-n+1).
Сочетаниями из m предметов по n называются группы, которые можно составить из m предметов таким образом, чтобы каждая группа заключала в себе n предметов и все такие группы отличались бы одна от другой предметами в них входящими. Число сочетаний из m по n обозначается символом Cnm и доказывается, что Cnm = [m(т —1)(т)...(m-n+1)]/1.2.3... п.
Перестановками из n предметов называются группы, которые можно составить из n предметов таким образом, чтобы все n предметов входили в каждую группу и одна группа от другой отличалась бы порядком распределения предметов. Число всех возможных перестановок из n предметов обозначается символом Pn и доказывается, что Pn = 1.2.3.4...n. Вычисление чисел Anm, Cnm, и Pn при больших m и n обыкновенным способом по приведенным формулам весьма затруднительно. В таких случаях удобнее пользоваться формулой Гудермана:
В К. анализе употребляются три метода: прямой, способ производящих функций Лапласа и формулы теории конечных разностей.
Н. Д.
|
Page was updated:Tuesday, 11-Sep-2012 18:15:37 MSK |