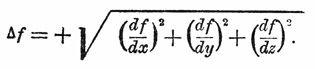
| [ начало ] | [ С ] |
Связь механическая
(Liaison, The connexion) — под механическими или кинематическими связями подразумеваются объекты, предметы, а иногда в механизмы, стесняющие или уменьшающие свободу (см.) движения материальных точек и тел. Одна реальная точка будет иметь две степени свободы, если она будет принуждена оставаться на данной поверхности; пусть уравнение этой поверхности f(x, у, z) = 0. С. называется удерживающей и уравнение поверхности, подразумевая в нем под x, y, z координаты материальной точки, представляет аналитическое выражение этой С. Если поверхность, выражаемая вышеприведенным уравнением, представляет собой только преграду движению точки, так что последняя может быть или на самой поверхности, или в тех частях пространства, координаты точек которого делают f (х, y, z) большей нуля, то такая преграда представляет С. неудерживающую, выражаемую условием: f(x,y,z)> 0 или = 0. Эта поверхность не препятствует точке сойти с нее в одну сторону, но не позволяет пройти через нее по ту сторону, где f (x, у,z)<0. Вполне твердый, нерастяжимый и несжимаемый стержень длины L, связывающий две материальные точки т 1 и m2, иаходящиеся на концах его, есть удерживающая связь между ними, выражаемая равенством:
L2 — (x1 — x2)2 — (y1 — y2)2 — (z1 — z2)2 = 0,
где точки x1, у 1, z1 суть координаты точки т 1, x2, у 2, z2 координаты точки т 2. Гибкая, но нерастяжимая нить, связывающая две точки m1 и m2 есть С. неудерживающая, выражаемая условием:
L2 — (x1 — x2)2 — (y1 — y2)2 — (z1 — z2)2 > 0 или = 0.
Вообще, всякая удерживающая С., связывающая точки m1, m2,...mn, может быть выражена равенством:
F(x1, y1, z1, x2, у 2, z2,..., zn) = 0,
где F есть некоторая функция, определяемая родом и видом С. Всякая неудерживающая С. между теми же точками может быть выражена условием вида:
F(x1, y1, z1, x2, у 2, z2,..., zn) > 0 или <0.
Дифференциальные параметры связей. Дифференциальным параметром удерживающей поверхности f(x, у,z) = 0 называется положительная величина:
Под направлением дифференциального параметра подразумевается направление нормали, восстановленной из места точки на поверхности в ту сторону пространства, где находятся точки, координаты которых делают f(x,y,z) большей нуля. Дифференциальный параметр неудерживающей поверхности направлен в свободную сторону. Связь, связывающая несколько точек m1, m2,...mi, mn, имеет особый дифференциальный параметр для каждой из точек. Дифференциальный параметр точки m, имеет положительную величину:
и направление его составляет с осями координат углы, косинусы которых равны отношениям: 1/ Pi dF/dxi, 1/Pi dF/dyi, 1/Pi dF/dzi.
Д. Б.
|
Page was updated:Tuesday, 11-Sep-2012 18:16:27 MSK |