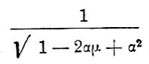
| [ начало ] | [ С ] |
Сферические функции
(Kugelfunctionen). — Выражение:
в котором α меньше единицы, a μ = Cos θ есть косинус некоторого угла θ, может быть разложено в следующий ряд, расположенный по возрастающим степеням а:
1 + аР 1 + а 2 Р 2 + а 3P3 +... + anPn +...,
в котором Ρ с разными индексами суть следующие функции от μ:
P1 = μ, P2 = (1/2)(3 μ 2 — 1)
P3 = (1/2)(5 μ 3 — 3 μ)...
и вообще Р n может быть представлено так:
Р n = (1/2nn!)(dn/d μ n)(μ 2 — 1)n, где п ! = 1.2.3...n.
Функции эти, введенные Лапласом при рассмотрении вопросов о притяжении, носят название С. функций. Полную теорию этих функций можно найти в книге Heine "Handbuch d. Kugelfunctionen", a в книгах Thomson and Тait ("Treatise on natural philosophy"), Lamb ("Hydrodynamics", 1895) и Cl. Maxwell, "Trait é d'électricité et de magnétisme" (trad. p. Lui Sé ligmann) объяснено значение этих функций в теории потенциала, притяжения, электричества, магнетизма и в гидродинамике; там же полная и рациональная теория С. функций.
Д. Б.
|
Page was updated:Tuesday, 11-Sep-2012 18:16:37 MSK |