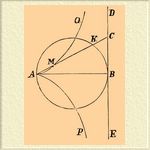
— была изобретена Диоклом (см.). Она получается при помощи следующего построения. Представим себе круг, касающейся прямой DBE в точке В. Через точку А, конец диаметра АВ, проведем луч АС до пересечения с прямой DBE в точке С.

Обозначим буквою К точку пересечения этого луча с окружностью данного круга. Если на АС отложим отрезок АМ = КС, то получим точку X, принадлежащую Ц.

Уравнение этой кривой, отнесенной к прямоугольной системе координат, имеет вид

Здесь a — радиус круга АКВ; начало координат взято в точке Α и ось x- ов совпадает с прямою AB.

Точка А есть точка возврата кривой, а de — ее прямолинейная асимптота.

Площадь, ограниченная кривою PAQ и ее асимптотой DE, равна 3 π a².